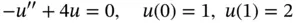(1.77) 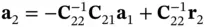
we get
(1.78) 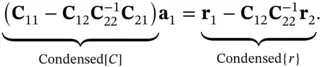
The condensed stiffness matrices and load vectors are assembled and the Dirichlet boundary conditions are enforced as described in the following section. Upon solving the assembled system of equations the coefficients of the internal basis functions are computed from eq. (1.77)for each element.
1.3.7 Enforcement of Dirichlet boundary conditions
When Dirichlet conditions are specified on either or both boundary points then 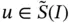 is split into two functions; a function
is split into two functions; a function 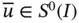 and an arbitrary specific function from
and an arbitrary specific function from 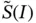 , denoted by
, denoted by 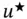 . We then seek
. We then seek 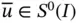 such that
such that
(1.79) 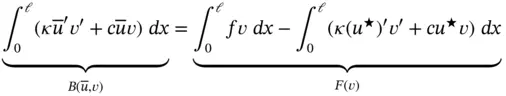
for all 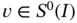 . Observe that the solution
. Observe that the solution 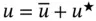 is independent of the choice of
is independent of the choice of  .
.
We denote the global numbers of the basis functions that are unity at  and
and 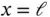 by K and L respectively. For instance, in Example 1.6
by K and L respectively. For instance, in Example 1.6 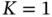 and
and 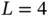 . It is advantageous to define
. It is advantageous to define 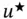 in terms of
in terms of 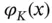 and
and 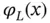 :
:
(1.80) 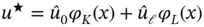
as indicated in Fig. 1.6. When Dirichlet boundary condition is prescribed on only one of the boundary points then this expression is modified to include the term corresponding to that point only.
On substituting eq. (1.80)into eq. (1.79)the second term on the right‐hand side of eq. (1.79)can be written as
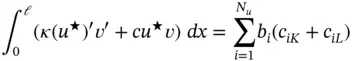
where Nu is the number of unconstrained equations, that is, the number of equations prior to enforcement of the Dirichlet boundary conditions. (For instance, in Example 1.6 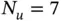 .) The coefficients
.) The coefficients 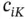 ,
, 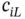 are elements of the assembled coefficient matrix.
are elements of the assembled coefficient matrix.
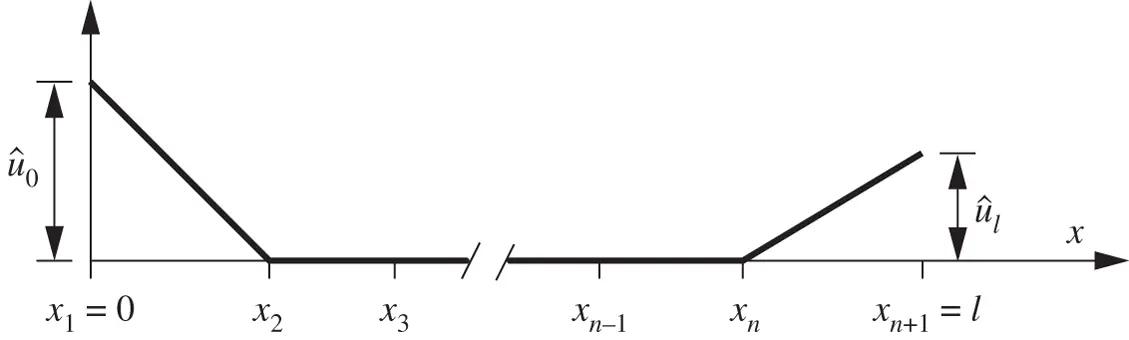
Figure 1.6 Recommended choice of the function 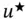 in one dimension.
in one dimension.
Since 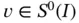 , we have
, we have 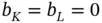 and therefore the K th and L th rows of matrix
and therefore the K th and L th rows of matrix  are multiplied by zero and can be deleted. The K th and L th columns of matrix
are multiplied by zero and can be deleted. The K th and L th columns of matrix 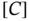 are multiplied by
are multiplied by 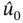 and
and 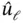 respectively, summed and the resulting vector is transferred to the right‐hand side. The resulting coefficient matrix has the dimension N which is Nu minus the number of Dirichlet boundary conditions. The number N is called the number of degrees of freedom. It is the maximum number of linearly independent functions in
respectively, summed and the resulting vector is transferred to the right‐hand side. The resulting coefficient matrix has the dimension N which is Nu minus the number of Dirichlet boundary conditions. The number N is called the number of degrees of freedom. It is the maximum number of linearly independent functions in 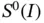 .
.
Remark 1.7In order to avoid having to renumber the coefficient matrix once the rows and columns corresponding to φK and φL were eliminated, all elements in the K th and L th rows and columns can be set to zero, with the exception of the diagonal elements, which are set to unity. The corresponding elements on the right hand side vector are set to û 0and ûℓ . This is illustrated by the following example.
Example 1.7Consider the problem
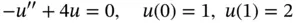
the exact solution of which is
Читать дальше

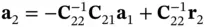
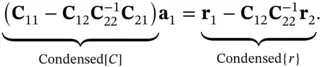
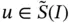 is split into two functions; a function
is split into two functions; a function 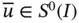 and an arbitrary specific function from
and an arbitrary specific function from 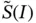 , denoted by
, denoted by 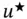 . We then seek
. We then seek 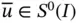 such that
such that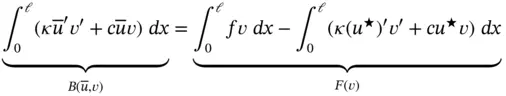
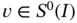 . Observe that the solution
. Observe that the solution 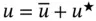 is independent of the choice of
is independent of the choice of  .
.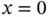 and
and 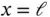 by K and L respectively. For instance, in Example 1.6
by K and L respectively. For instance, in Example 1.6 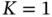 and
and 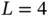 . It is advantageous to define
. It is advantageous to define 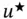 in terms of
in terms of 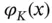 and
and 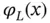 :
: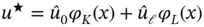
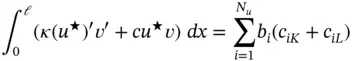
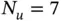 .) The coefficients
.) The coefficients 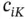 ,
, 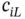 are elements of the assembled coefficient matrix.
are elements of the assembled coefficient matrix.
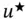 in one dimension.
in one dimension.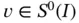 , we have
, we have 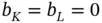 and therefore the K th and L th rows of matrix
and therefore the K th and L th rows of matrix  are multiplied by zero and can be deleted. The K th and L th columns of matrix
are multiplied by zero and can be deleted. The K th and L th columns of matrix 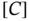 are multiplied by
are multiplied by 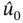 and
and 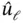 respectively, summed and the resulting vector is transferred to the right‐hand side. The resulting coefficient matrix has the dimension N which is Nu minus the number of Dirichlet boundary conditions. The number N is called the number of degrees of freedom. It is the maximum number of linearly independent functions in
respectively, summed and the resulting vector is transferred to the right‐hand side. The resulting coefficient matrix has the dimension N which is Nu minus the number of Dirichlet boundary conditions. The number N is called the number of degrees of freedom. It is the maximum number of linearly independent functions in 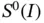 .
.