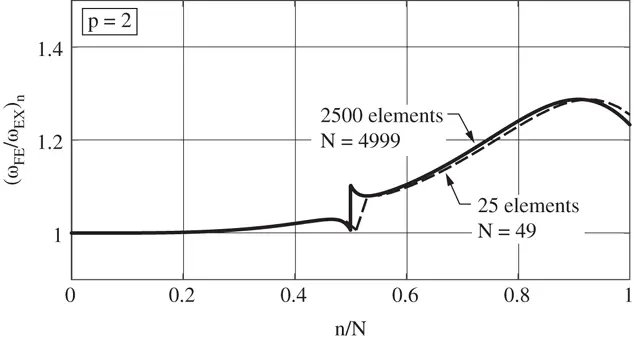
Figure 1.13 The ratio 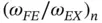 corresponding to the h version,
corresponding to the h version, 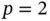 .
.
If we approximate the eigenfunctions using a uniform mesh consisting of 5 elements, and increase the polynomial degrees uniformly then we get the curves shown in Fig. 1.14. The curves show that only about 40% of the numerically computed eigenvalues will be accurate. The error increases monotonically for the higher eigenvalues and the size of the error is virtually independent of p .
It is possible to reduce this error by enforcing the continuity of derivatives. Examples are available in [32]. There is a tradeoff, however: Enforcing continuity of derivatives on the basis functions reduces the number of degrees of freedom but entails a substantial programming burden because an adaptive scheme has to be devised for the general case to ensure that the proper degree of continuity is enforced. If, for example, μ would be a piecewise constant function then the continuity of the first and higher derivatives must not be enforced in those points where μ is discontinuous.
From the perspective of designing a finite element software, it is advantageous to design the software in such a way that it will work well for a broad class of problems. In the formulation presented in this chapter 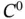 continuity is a requirement. Functions that lie in
continuity is a requirement. Functions that lie in 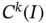 where
where 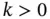 are also in
are also in 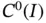 . In other words, the space
. In other words, the space 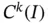 is embedded in the space
is embedded in the space 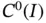 . Symbolically:
. Symbolically: 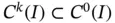 . The exact eigenfunctions in this example are in
. The exact eigenfunctions in this example are in 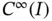 .
.
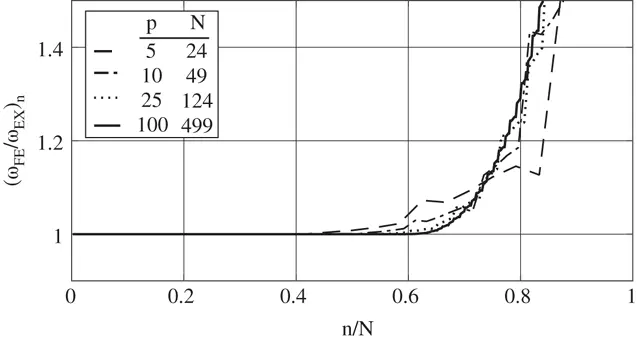
Figure 1.14 The ratio 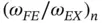 corresponding to the p version. Uniform mesh, 5 elements.
corresponding to the p version. Uniform mesh, 5 elements.
Table 1.6 Example: p ‐Convergence of the 24th eigenvalue in Example 1.16.
| p |
5 |
10 |
15 |
20 |
| ω 24 |
194.296 |
100.787 |
98.312 |
98.312 |
Example 1.16 Let us consider the problem in Example 1.15modified so that μ is a piecewise constant function defined on a uniform mesh of 5 elements such that 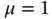 on elements 1, 3 and 5,
on elements 1, 3 and 5, 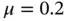 on elements 2 and 4. In this case the exact eigenfunctions are not smooth and the exact eigenvalues are not known explicitly.
on elements 2 and 4. In this case the exact eigenfunctions are not smooth and the exact eigenvalues are not known explicitly.
At 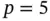 there are 24 degrees of freedom. Suppose that the 24th eigenvalue is of interest. If we increase p uniformly then this eigenvalue converges to 98.312. The results of computation are shown in Table 1.6.
there are 24 degrees of freedom. Suppose that the 24th eigenvalue is of interest. If we increase p uniformly then this eigenvalue converges to 98.312. The results of computation are shown in Table 1.6.
Any eigenvalue can be approximated to an arbitrary degree of precision on a suitably defined mesh and uniform increase in the degrees of freedom. When κ and/or 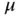 are discontinuous functions then the points of discontinuity must be node points.
are discontinuous functions then the points of discontinuity must be node points.
Observe that the numerically computed eigenvalues converge monotonically from above. This follows directly from the fact that the eigenfunctions are minimizers of the Rayleigh quotient.
Exercise 1.21Prove eq. (1.143).
Exercise 1.22Find the eigenvalues for the problem of Example 1.15using the generalized formulation and the basis functions 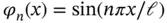 , (
, ( 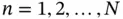 ). Assume that κ and
). Assume that κ and 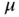 are constants and
are constants and 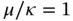 . Let
. Let 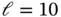 . Explain what makes this choice of basis functions very special. Hint: Owing to the orthogonality of the basis functions, only hand calculations are involved.
. Explain what makes this choice of basis functions very special. Hint: Owing to the orthogonality of the basis functions, only hand calculations are involved.
1.8 Other finite element methods
Up to this point we have been concerned with the finite element method based on the generalized formulation, called the principle of virtual work. There are many other finite element methods. All finite element methods share the following attributes:
1 Formulation. A bilinear form is defined on the normed linear spaces X, Y (i.e. , ) and the functional is defined on Y. The exact solution lies in X and satisfies:(1.151) The normed linear spaces, , the linear functional F and the bilinear form B satisfy the respective properties listed in sections A.1.1and A.1.2.
2 Finite element spaces. The finite‐dimensional subspaces , () are defined and it is assumed that there are such that the sequence of functions ûi () converges in the space X to , that is:(1.152) The functions ûi are not the finite element solutions in general.
3 The finite element solution. The finite element solution satisfies:(1.153)
4 The stability criterion. The finite element method is said to be stable if(1.154) for all possible . The necessary and sufficient condition for a finite element method to be stable is that for every there is a so that(1.155) where is a constant, independent of i, or for every there is a so that this inequality holds. This inequality is known as the Babuška‐Brezzi condition, usually abbreviated to “the BB condition”. This condition was formulated by Babuška in 1971 [9] and independently by Brezzi in 1974 [29].
Читать дальше


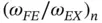 corresponding to the h version,
corresponding to the h version, 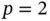 .
.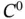 continuity is a requirement. Functions that lie in
continuity is a requirement. Functions that lie in 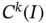 where
where 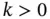 are also in
are also in 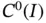 . In other words, the space
. In other words, the space 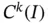 is embedded in the space
is embedded in the space 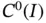 . Symbolically:
. Symbolically: 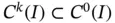 . The exact eigenfunctions in this example are in
. The exact eigenfunctions in this example are in 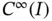 .
.
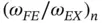 corresponding to the p version. Uniform mesh, 5 elements.
corresponding to the p version. Uniform mesh, 5 elements.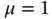 on elements 1, 3 and 5,
on elements 1, 3 and 5, 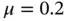 on elements 2 and 4. In this case the exact eigenfunctions are not smooth and the exact eigenvalues are not known explicitly.
on elements 2 and 4. In this case the exact eigenfunctions are not smooth and the exact eigenvalues are not known explicitly.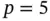 there are 24 degrees of freedom. Suppose that the 24th eigenvalue is of interest. If we increase p uniformly then this eigenvalue converges to 98.312. The results of computation are shown in Table 1.6.
there are 24 degrees of freedom. Suppose that the 24th eigenvalue is of interest. If we increase p uniformly then this eigenvalue converges to 98.312. The results of computation are shown in Table 1.6.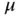 are discontinuous functions then the points of discontinuity must be node points.
are discontinuous functions then the points of discontinuity must be node points.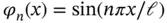 , (
, ( 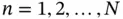 ). Assume that κ and
). Assume that κ and 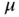 are constants and
are constants and 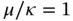 . Let
. Let 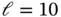 . Explain what makes this choice of basis functions very special. Hint: Owing to the orthogonality of the basis functions, only hand calculations are involved.
. Explain what makes this choice of basis functions very special. Hint: Owing to the orthogonality of the basis functions, only hand calculations are involved.










