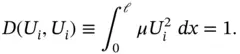
If the eigenvalues are distinct then the corresponding eigenfunctions are orthogonal: Let 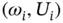 and
and 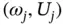 be eigenpairs,
be eigenpairs, 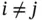 . Then from eq. (1.140)we have
. Then from eq. (1.140)we have
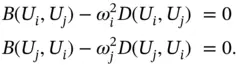
Subtracting the second equation from the first we see that if 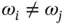 then Ui and Uj are orthogonal functions:
then Ui and Uj are orthogonal functions:
(1.141) 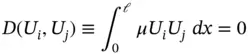
and hence 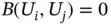 .
.
Importantly, it can be shown that any function 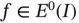 can be written as a linear combination of the eigenfunctions:
can be written as a linear combination of the eigenfunctions:
(1.142) 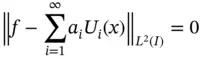
where
(1.143) 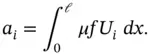
The Rayleigh 15 quotient is defined by
(1.144) 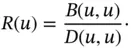
Eigenvalues are usually numbered in ascending order. Following that convention,
(1.145) 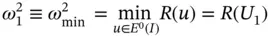
that is, the smallest eigenvalue is the minimum of the Rayleigh quotient and the corresponding eigenfunction is the minimizer of 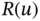 on
on 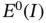 . This follows directly from eq. (1.140). The k th eigenvalue minimizes
. This follows directly from eq. (1.140). The k th eigenvalue minimizes 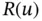 on the space
on the space 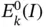
(1.146) 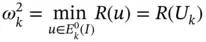
where
(1.147) 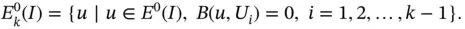
When the eigenvalues are computed numerically then the minimum of the Rayleigh quotient is sought on the finite‐dimensional space 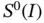 . We see from the definition
. We see from the definition 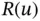 that the error of approximation in the natural frequencies will depend on how well the eigenfunctions are approximated in energy norm, in the space
that the error of approximation in the natural frequencies will depend on how well the eigenfunctions are approximated in energy norm, in the space 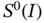 .
.
The following example illustrates that in a sequence of numerically computed eigenvalues only the lower eigenvalues will be approximated well. It is possible, however, at least in principle, to obtain good approximation for any eigenvalue by suitably enlarging the space 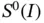 .
.
Example 1.15 Let us consider the eigenvalue problem
(1.148) 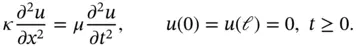
This equation models (among other things) the free vibration (natural frequencies and mode shapes) of a string of length 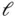 stretched horizontally by the force
stretched horizontally by the force 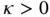 (N) under the assumptions that the displacements are infinitesimal and confined to one plane, the plane of vibration, and the ends of the string are fixed. The mass per unit length is
(N) under the assumptions that the displacements are infinitesimal and confined to one plane, the plane of vibration, and the ends of the string are fixed. The mass per unit length is 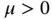 (kg/m). We assume that κ and
(kg/m). We assume that κ and 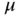 are constants. It is left to the reader to verify that the function u defined by
are constants. It is left to the reader to verify that the function u defined by
(1.149) 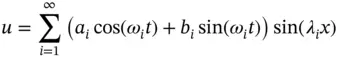
where ai , bi are coefficients determined from the initial conditions and
(1.150) 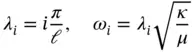
satisfies eq. (1.148).
If we approximate the eigenfunctions using uniform mesh,  and plot the ratio
and plot the ratio 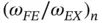 against
against 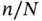 , where n is the n th eigenvalue, then we get the curves shown in Fig. 1.13. The curves show that somewhat more than 20% of the numerically computed eigenvalues will be accurate. The higher eigenvalues cannot be well approximated in the space
, where n is the n th eigenvalue, then we get the curves shown in Fig. 1.13. The curves show that somewhat more than 20% of the numerically computed eigenvalues will be accurate. The higher eigenvalues cannot be well approximated in the space 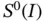 . The existence of the jump seen at
. The existence of the jump seen at 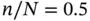 is a feature of numerically approximated eigenvalues by means of standard finite element spaces using the h ‐version [2]. The location of the jump depends on the polynomial degree of elements. There is no jump when
is a feature of numerically approximated eigenvalues by means of standard finite element spaces using the h ‐version [2]. The location of the jump depends on the polynomial degree of elements. There is no jump when 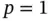 .
.
Читать дальше

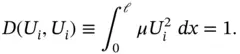
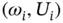 and
and 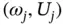 be eigenpairs,
be eigenpairs, 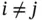 . Then from eq. (1.140)we have
. Then from eq. (1.140)we have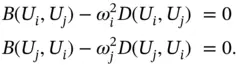
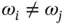 then Ui and Uj are orthogonal functions:
then Ui and Uj are orthogonal functions: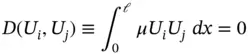
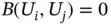 .
.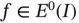 can be written as a linear combination of the eigenfunctions:
can be written as a linear combination of the eigenfunctions: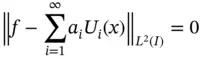
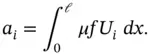
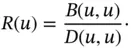
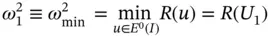
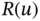 on
on 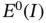 . This follows directly from eq. (1.140). The k th eigenvalue minimizes
. This follows directly from eq. (1.140). The k th eigenvalue minimizes 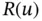 on the space
on the space 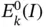
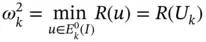
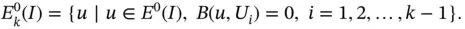
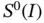 . We see from the definition
. We see from the definition 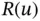 that the error of approximation in the natural frequencies will depend on how well the eigenfunctions are approximated in energy norm, in the space
that the error of approximation in the natural frequencies will depend on how well the eigenfunctions are approximated in energy norm, in the space 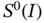 .
.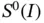 .
.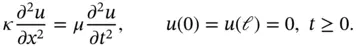
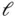 stretched horizontally by the force
stretched horizontally by the force 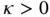 (N) under the assumptions that the displacements are infinitesimal and confined to one plane, the plane of vibration, and the ends of the string are fixed. The mass per unit length is
(N) under the assumptions that the displacements are infinitesimal and confined to one plane, the plane of vibration, and the ends of the string are fixed. The mass per unit length is 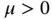 (kg/m). We assume that κ and
(kg/m). We assume that κ and 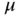 are constants. It is left to the reader to verify that the function u defined by
are constants. It is left to the reader to verify that the function u defined by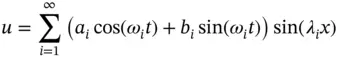
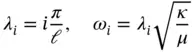
 and plot the ratio
and plot the ratio 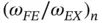 against
against 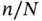 , where n is the n th eigenvalue, then we get the curves shown in Fig. 1.13. The curves show that somewhat more than 20% of the numerically computed eigenvalues will be accurate. The higher eigenvalues cannot be well approximated in the space
, where n is the n th eigenvalue, then we get the curves shown in Fig. 1.13. The curves show that somewhat more than 20% of the numerically computed eigenvalues will be accurate. The higher eigenvalues cannot be well approximated in the space 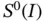 . The existence of the jump seen at
. The existence of the jump seen at 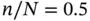 is a feature of numerically approximated eigenvalues by means of standard finite element spaces using the h ‐version [2]. The location of the jump depends on the polynomial degree of elements. There is no jump when
is a feature of numerically approximated eigenvalues by means of standard finite element spaces using the h ‐version [2]. The location of the jump depends on the polynomial degree of elements. There is no jump when 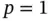 .
.










