3 is the set of functions which are linear on every element and discontinuous at the nodes (dimension ).
For these choices of 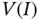 the mixed formulation leads to systems of linear equations with
the mixed formulation leads to systems of linear equations with 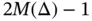 ,
, 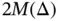 and
and 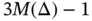 unknowns, respectively. In the cases
unknowns, respectively. In the cases 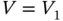 and
and 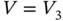 , a constant C exists such that the inequality (1.163)holds for all
, a constant C exists such that the inequality (1.163)holds for all 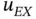 , and
, and 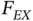 . In the case of
. In the case of 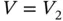 , however, such a constant does not exist. This means that no matter how large C is, there exist some
, however, such a constant does not exist. This means that no matter how large C is, there exist some 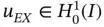 and
and 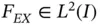 and mesh
and mesh  so that the inequality (1.163)is not satisfied. On the other hand, there will be
so that the inequality (1.163)is not satisfied. On the other hand, there will be 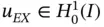 and
and 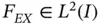 for which the inequality is satisfied and therefore the finite element solutions will converge to the underlying exact solution.
for which the inequality is satisfied and therefore the finite element solutions will converge to the underlying exact solution.
Nitsche's method 16 allows the treatment of essential boundary conditions as natural boundary conditions. This has certain advantages in two and three dimensions. An outline of the algorithmic aspects of the method is presented in the following. For additional details we refer to [51].
Consider the problem:
(1.164) 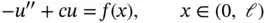
with the boundary conditions 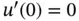 and
and 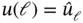 . However, at
. However, at 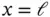 we substitute the natural boundary condition:
we substitute the natural boundary condition:
(1.165) 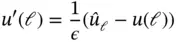
where 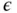 is a small positive number,
is a small positive number, 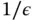 is called penalty parameter. The role of the penalty parameter becomes clearly visible if we consider the potential energy
is called penalty parameter. The role of the penalty parameter becomes clearly visible if we consider the potential energy
(1.166) 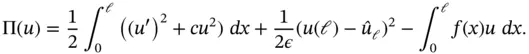
Letting 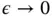 , the minimizer of the potential energy converges to the solution of the Dirichlet problem; however, the numerical problem becomes ill‐conditioned. Nitsche's method stabilizes the numerical problem making it possible to solve it for the full range of boundary conditions, including
, the minimizer of the potential energy converges to the solution of the Dirichlet problem; however, the numerical problem becomes ill‐conditioned. Nitsche's method stabilizes the numerical problem making it possible to solve it for the full range of boundary conditions, including 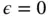 .
.
On multiplying eq. (1.164)by v and integrating by parts we get
(1.167) 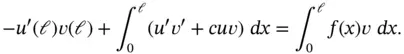
We introduce the stability parameter γ and multiply eq. (1.165)by 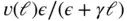 to get
to get
(1.168) 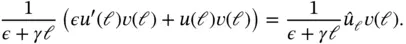
Adding eq. (1.167)and eq. (1.168)we get
(1.169) 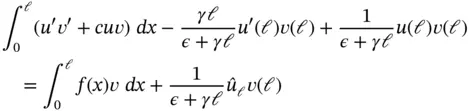
and, multiplying eq. (1.165)by 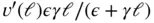 , we have
, we have
(1.170) 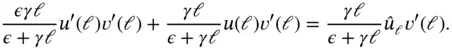
Subtracting eq. (1.170)from eq. (1.169)we obtain the generalized formulation:
(1.171) 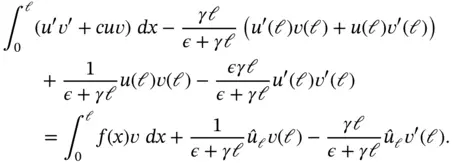
Letting 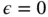 in eq. (1.171)we get the stabilized method proposed by Nitsche [67]:
in eq. (1.171)we get the stabilized method proposed by Nitsche [67]:
(1.172) 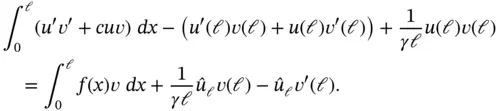
Letting 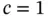 ,
, 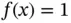 ,
, 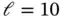 and
and 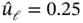 we construct the numerical problem using one element and the hierarchic shape functions defined in Section 1.3.1. By definition:
we construct the numerical problem using one element and the hierarchic shape functions defined in Section 1.3.1. By definition:
Читать дальше

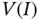 the mixed formulation leads to systems of linear equations with
the mixed formulation leads to systems of linear equations with 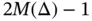 ,
, 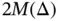 and
and 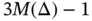 unknowns, respectively. In the cases
unknowns, respectively. In the cases 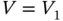 and
and 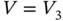 , a constant C exists such that the inequality (1.163)holds for all
, a constant C exists such that the inequality (1.163)holds for all 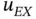 , and
, and 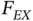 . In the case of
. In the case of 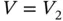 , however, such a constant does not exist. This means that no matter how large C is, there exist some
, however, such a constant does not exist. This means that no matter how large C is, there exist some 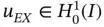 and
and 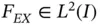 and mesh
and mesh  so that the inequality (1.163)is not satisfied. On the other hand, there will be
so that the inequality (1.163)is not satisfied. On the other hand, there will be 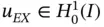 and
and 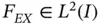 for which the inequality is satisfied and therefore the finite element solutions will converge to the underlying exact solution.
for which the inequality is satisfied and therefore the finite element solutions will converge to the underlying exact solution.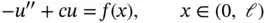
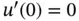 and
and 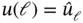 . However, at
. However, at 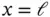 we substitute the natural boundary condition:
we substitute the natural boundary condition: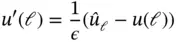
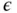 is a small positive number,
is a small positive number, 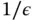 is called penalty parameter. The role of the penalty parameter becomes clearly visible if we consider the potential energy
is called penalty parameter. The role of the penalty parameter becomes clearly visible if we consider the potential energy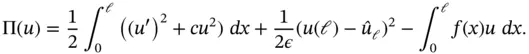
 , the minimizer of the potential energy converges to the solution of the Dirichlet problem; however, the numerical problem becomes ill‐conditioned. Nitsche's method stabilizes the numerical problem making it possible to solve it for the full range of boundary conditions, including
, the minimizer of the potential energy converges to the solution of the Dirichlet problem; however, the numerical problem becomes ill‐conditioned. Nitsche's method stabilizes the numerical problem making it possible to solve it for the full range of boundary conditions, including  .
.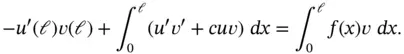
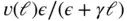 to get
to get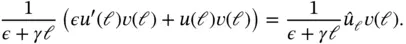
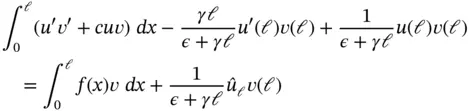
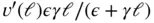 , we have
, we have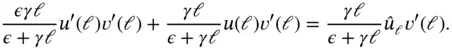
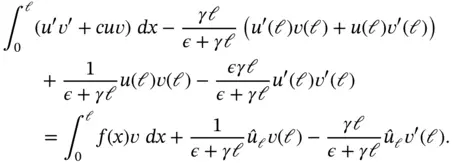
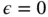 in eq. (1.171)we get the stabilized method proposed by Nitsche [67]:
in eq. (1.171)we get the stabilized method proposed by Nitsche [67]: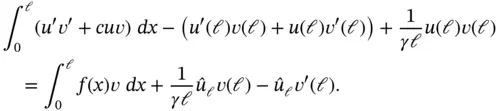
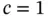 ,
, 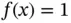 ,
, 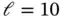 and
and 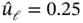 we construct the numerical problem using one element and the hierarchic shape functions defined in Section 1.3.1. By definition:
we construct the numerical problem using one element and the hierarchic shape functions defined in Section 1.3.1. By definition:










