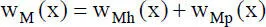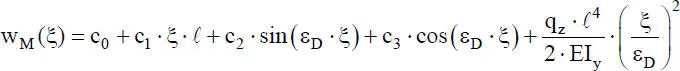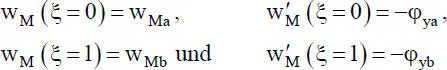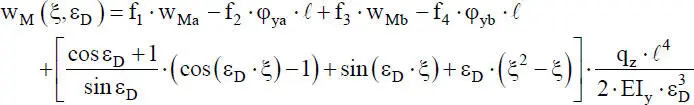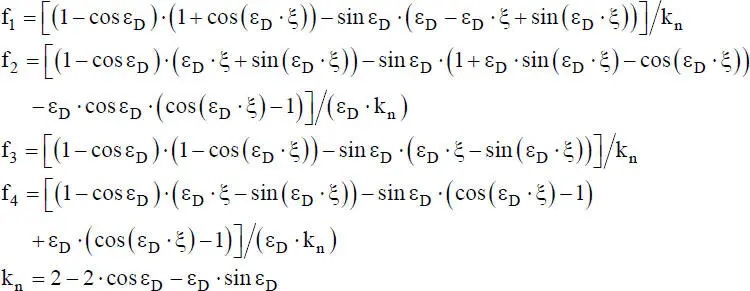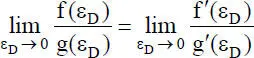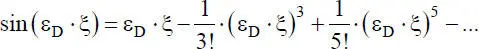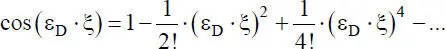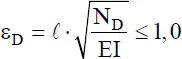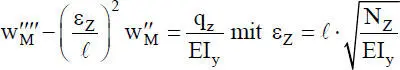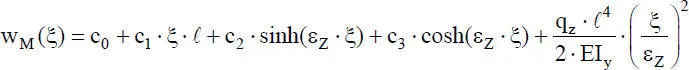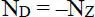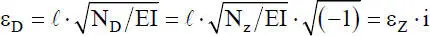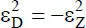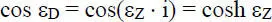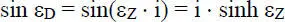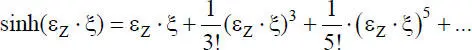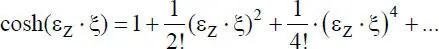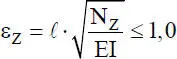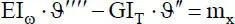(2.33) 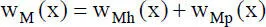
Der erste Term beschreibt die Lösung der homogenen DGL, also für q z= 0, und der zweite die partikuläre Lösung. Nach [26] erhält man mit x = ξ ⋅ ℓ :
(2.34) 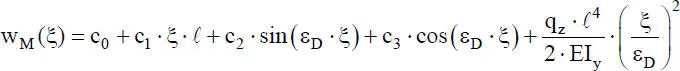
Wie in Abschnitt 2.5.2können die Integrationskonstanten c 0bis c 3durch ingenieurmäßig anschauliche Verformungsgrößen ersetzt werden. Mit
(2.35a-d) 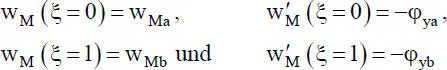
erhält man die folgende Funktion für die Durchbiegung eines Stabelementes, das durch eine Drucknormalkraft und eine Gleichstreckenlast beansprucht wird:
(2.36) 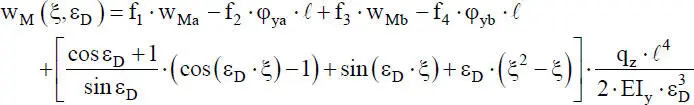
Mit:
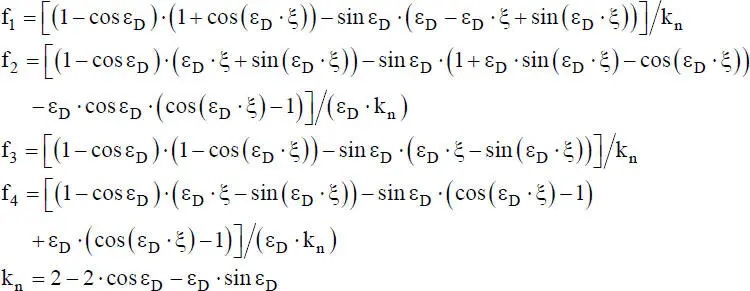
Gl. (2.36)für ein „Biegeknick-Stabelement“ ist im Vergleich zu Gl. (2.31)für das rein auf Biegung beanspruchte Stabelement wesentlich länger und daher im Hinblick auf die weitere Verwendung erheblich aufwändiger. Bei der FEM wird sie jedoch erfreulicherweise nur selten benötigt. An dieser Stelle soll nur gezeigt werden, wie die genaue Lösung der Verformungsfunktion für das Biegeknicken lautet. In Abschnitt 4.6wird die genaue Lösung der DGL zur Herleitung der Steifigkeitsmatrix nach Theorie II. Ordnung erneut herangezogen.
Mit N = 0 bzw. ε D= 0 kann Gl. (2.36)in Gl. (2.31)überführt werden. Dies ist allerdings nicht unmittelbar durch Einsetzen möglich, weil unbestimmte Ausdrücke der Form „0/0“ auftreten. Auch die Lösung mit der Grenzwertregel von Bernoulli und del´Hospital
(2.37) 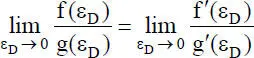
ist aufwändig und in der Regel mehrmals anzuwenden. Mit den Reihenentwicklungen
(2.38) 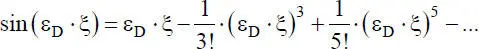
(2.39) 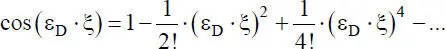
für die trigonometrischen Funktionen ist der Zusammenhang zwischen den Gl. (2.36)und (2.31)erkennbar. Da Gl. (2.36)für ε D→ 0 in Gl. (2.31)übergeht, kann Gl. (2.36)für kleine Stabkennzahlen näherungsweise durch die Polynomfunktion, ersetzt werden. Durch eine entsprechend feine FE-Modellierung kann man stets erreichen, dass ε Dklein ist, weil bei diesem Parameter die Elementlänge ℓ eingeht. Wie in Abschnitt 4.6näher erläutert, ist die Näherung mit der Polynomfunktion Gl. (2.31)aus-reichend genau, wenn die Bedingung
(2.40) 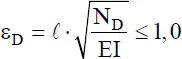
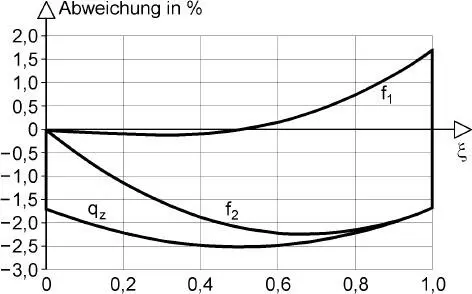
Bild 2.13 Vergleich der Polynomfunktion Gl. (2.31)mit Gl. (2.36)für ε D= 1
eingehalten wird. Bild 2.13zeigt die Abweichung zwischen der Polynomfunktion in Bezug auf die genaue Durchbiegungsfunktion Gl. (2.36)für ε D= 1. Die Funktionen f 3und f 4sind nicht dargestellt, da die Abweichungen denen der Funktionen f 1und f 2entsprechen, siehe auch Bild 2.12. Wie man sieht sind die Abweichungen mit bis zu 2,5 % gering.
Biegung mit Zugnormalkraft nach Theorie II. Ordnung
Im Vergleich zu dem zuvor behandelten Beanspruchungsfall mit einer Drucknormalkraft wird hier der Einfluss einer Zugnormalkraft untersucht. Für die DGL (2.16)
(2.41) 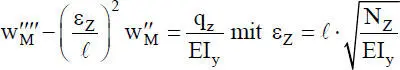
ergibt sich als Lösung
(2.42) 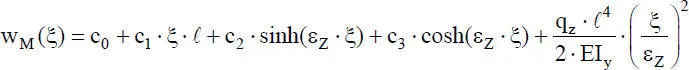
Alle Lösungen für die Theorie II. Ordnung mit Druckkraft (ND) können in Lösungen für die Theorie II. Ordnung mit Zugkraft (NZ) umgerechnet werden. Mit
(2.43) 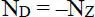
erhält man
(2.44) 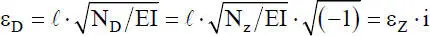
In Gl. (2.44)ist „i“ die imaginäre Einheit mit i 2= ‒1. Bei der Umrechnung werden in der Regel nur folgende Beziehungen benötigt:
(2.45) 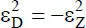
(2.46) 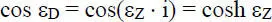
(2.47) 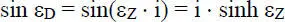
Mit diesen Beziehungen kann Gl. (2.36)problemlos umgerechnet werden, worauf hier jedoch verzichtet wird. Zur Vervollständigung seien auch die Reihenentwicklungen der Hyperbelfunktionen angegeben:
(2.48) 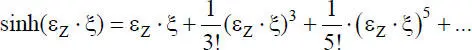
(2.49) 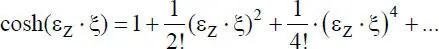
Auch bei der Theorie II. Ordnung mit Zugnormalkraft kann eine Näherung mit der Polynomfunktion (2.31)verwendet werden. Bei der Wahl der Elementlänge ℓ ist dann die Bedingung
(2.50) 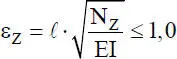
zu beachten. Auf weitere Einzelheiten zur Verwendung der Näherung wird in Abschnitt 4.6eingegangen.
Wölbkrafttorsion
Für die Wölbkrafttorsion ergibt sich mit Tabelle 2.3und der Annahme konstanter Steifigkeiten im Stabelement die folgende DGL:
(2.51) 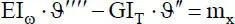
Читать дальше