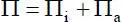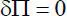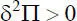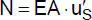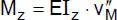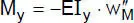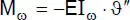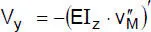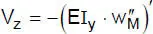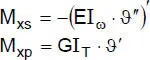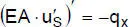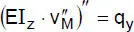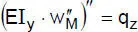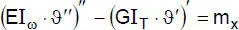Matthias Krauß - Finite-Elemente-Methoden im Stahlbau

Tabelle 2.2 Virtuelle Arbeit bei Stäben nach Theorie I. Ordnung (lineare Stabtheorie)

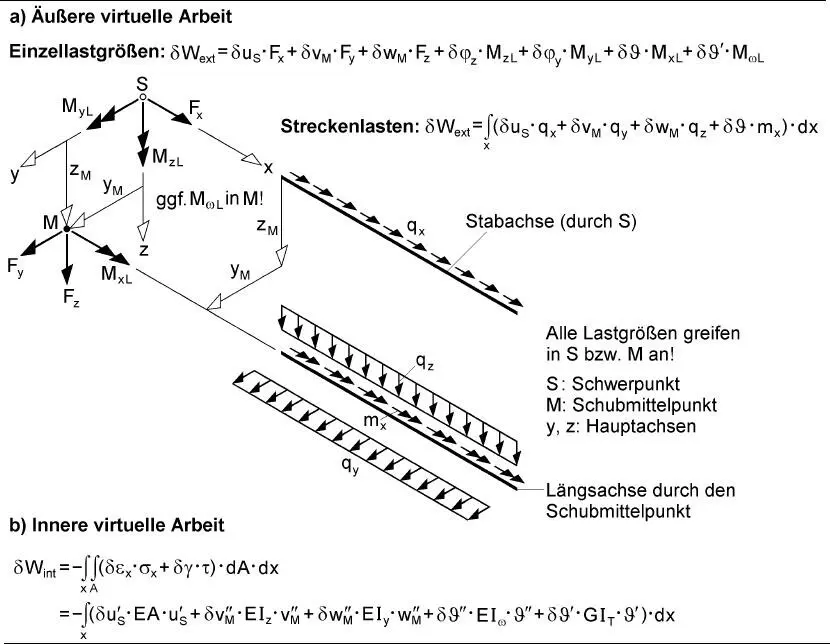
Die virtuelle Arbeit wird für Stäbe in [12] ausführlich hergeleitet und kann übernommen werden. Tabelle 2.2enthält eine Zusammenstellung für die lineare Stabtheorie (Theorie I. Ordnung). Dabei ist zu beachten, dass alle Lastgrößen im Schwerpunkt bzw. Schubmittelpunkt angreifen und die Richtungen den Hauptachsen entsprechen. Sofern das nicht der Fall ist, sind vorab entsprechende Transformationen durchzuführen, siehe dazu auch Abschnitt 3.4. Die virtuelle Arbeit für Federn und Schubfelder werden in Abschnitt 3.10und zusätzliche Arbeitsanteile für die Theorie II. Ordnung und Stabilität in Kapitel 4zusammengestellt. Für Stabquerschnitte wird die virtuelle Arbeit in Kapitel 7dargestellt.

Unter dem Begriff Energie versteht man die von einem System gespeicherte Arbeit . Wird durch eine Kraft die Verschiebung eines Körpers hervorgerufen, verrichtet sie Arbeit am Körper, die als potentielle Energie (Lageenergie) in diesem gespeichert wird. Die gesamte potentielle Energie Π (Gesamtpotential) eines Systems setzt sich aus der Formänderungsenergie Πi (innere Energie bzw. inneres Potential ) und der Energie der äußeren Kräfte (äußeres Potential ) Π azusammen:

(2.9)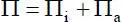

Bei baustatischen Systemen handelt es sich im Allgemeinen um sogenannte konservative Systeme, d. h. um solche mit konservativen Kräften . Eine Kraft wird als konservativ bezeichnet, wenn die Größe der von ihr geleisteten Arbeit an einem Massenpunkt unabhängig vom Weg ist. Anders ausgedrückt ist die Arbeit, die durch die Verschiebung des Massenpunktes von einer Stelle zu einer anderen geleistet wird, immer die gleiche, egal welcher Weg dabei zurückgelegt wird. Handelt es sich um einen geschlossenen Weg, also eine Verformung zurück in die Ursprungslage, ist für konservative Kräfte die gesamte Arbeit gleich null.

Das Prinzip vom Minimum der potentiellen Energie, das auch Dirichletsches Variationsprinzip genannt wird, besagt, dass für alle geometrisch möglichen Verschiebungszustände der wahre Zustand eines konservativen Systems, bei dem es sich somit im Gleichgewicht befindet, die potentielle Energie zu einem Minimum macht (energetisches Extremalprinzip):

(2.10)

Mit der 1. Variation des Gesamtpotentials kann die notwendige Bedingung

(2.11)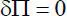

und mit der 2. Variation die hinreichende Bedingung

(2.12)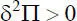

für die Existenz eines Minimums angegeben werden. Zur Verformung eines Systems muss mit δΠ = 0 und δ 2Π > 0 eine geringe Arbeit aufgebracht werden – das System befindet sich in einem stabilen Gleichgewichtszustand. Ist dagegen δ 2Π = 0, kann der Verformungszustand ohne Arbeitsaufwand variiert werden (indifferentes Gleichgewicht) und für δ 2Π < 0 wird vom System Energie freigesetzt (labiles Gleichgewicht). In Bild 2.10werden die grundlegenden Zusammenhänge nach [53] wiedergegeben. Eine detaillierte Darstellung der Potentiale und deren Variation soll an dieser Stelle nicht vorgenommen, sondern kann beispielsweise [1], [31], [53] und [49] entnommen werden. Als Ergebnis zeigt sich, dass bei konservativen Systemen die 1. Variation des Gesamtpotentials der virtuellen Arbeit entspricht. Beide Prinzipien sind äquivalent, wobei aufgrund der Extremaleigenschaft das Prinzip vom Minimum der potentiellen Energie zusätzlich die Aussage liefert, dass jede Näherungslösung für den Verformungszustand die potentielle Energie „von oben“ approximiert. Bei nichtkonservativen Systemen kann nur die virtuelle Arbeit für die Entwicklung von Näherungslösungen herangezogen werden.

Somit sind die virtuelle Arbeit und das Minimum der potentiellen Energie als Prinzi-pien für die Formulierung des Gleichgewichts für die hier behandelten Anwendungs-fälle gleichwertig. Da das Prinzip der virtuellen Arbeit etwas allgemeingültiger und für Ingenieure besser verständlich ist, wird es in dem vorliegenden Buch durchgängig verwendet.

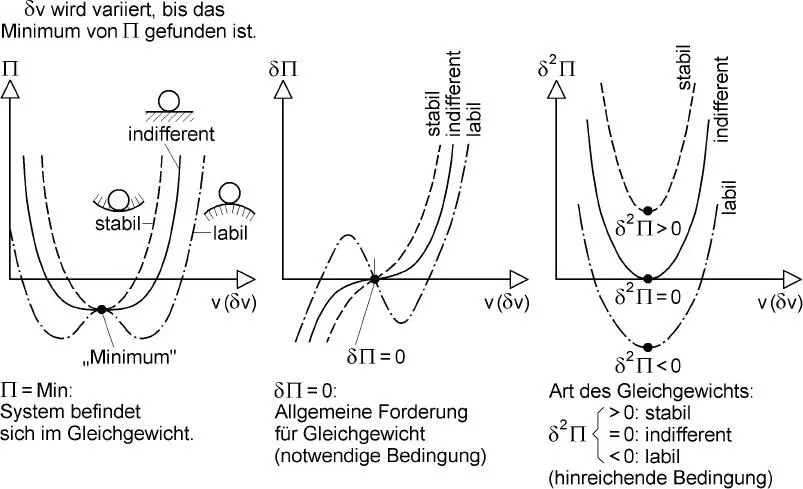
Bild 2.10 Grundsätzliche Zusammenhänge zum Prinzip vom Minimum der potentiellen Energie und Arten des Gleichgewichts nach [53]

Wie in den vorherigen Abschnitten bereits erwähnt, wird die virtuelle Arbeit zur For-mulierung des Gleichgewichts und der Elementsteifigkeitsmatrizen verwendet. Diffe-rentialgleichungen sind daher hier von nachrangiger Bedeutung. Andererseits erleich-tern sie das Verständnis für die mechanischen und baustatischen Zusammenhänge und sollen insbesondere zur Beurteilung der Ansatzfunktionen für die Verformungen ( Abschnitt 2.5) herangezogen werden. In [12] werden die Differentialgleichungen für die lineare Stabtheorie ausführlich hergeleitet. Dabei werden die virtuelle Arbeit, die Definition der Schnittgrößen und die am differentiellen Stababschnitt formulierten Gleichgewichtsbedingungen verwendet. Darüber hinaus gehen die nach der Elastizitätstheorie berechneten Spannungen σ xund τ ein. Tabelle 2.3enthält eine Zusammenstellung der Differentialgleichungen aus [12] für die lineare Stabtheorie, s. auch Tabelle 1.3.

Tabelle 2.3 Differentialgleichungen der linearen Stabtheorie (zweiachsige Biegung mit Normalkraft und Torsion)

„Normalkraft”	„Biegung um die z-Achse”	„Biegung um die y-Achse”	„Torsion”
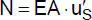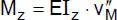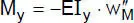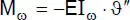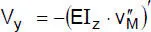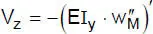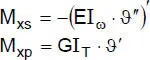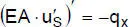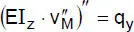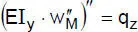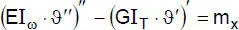mit: Elastizitätsmodul E, Schubmodul G, Querschnittsfläche A, Hauptträgheitsmomente I yund I z, minimaler Wölbwiderstand I ω, Torsionsträgheitsmoment I T

Bei Berechnungen nach Theorie II. Ordnung und zur Stabilität (Eigenwerte) ergeben sich erweiterte Differentialgleichungen. Nach [26] erhält man folgende Beziehungen zwischen Verschiebungs- und Lastgrößen: