(2.5) 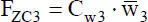
ersetzt werden. Sie korrespondiert zu 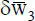 , so dass zu dem Hauptdiagonalelement in der 8. Zeile der Wert von C w3hinzu zu addieren ist.
, so dass zu dem Hauptdiagonalelement in der 8. Zeile der Wert von C w3hinzu zu addieren ist.
Der Vektor 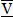 enthält die 15 Verschiebungsgrößen in den fünf Knoten, die in Bild 2.1ddargestellt sind. Im Gesamtlastvektor
enthält die 15 Verschiebungsgrößen in den fünf Knoten, die in Bild 2.1ddargestellt sind. Im Gesamtlastvektor 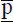 sind die Lastgrößen und die Auflagerreaktionen zusammengestellt. Dabei beziehen sich die Vorzeichen, wie bereits er-wähnt, auf das globale X-Z-KOS in Bild 2.1b.
sind die Lastgrößen und die Auflagerreaktionen zusammengestellt. Dabei beziehen sich die Vorzeichen, wie bereits er-wähnt, auf das globale X-Z-KOS in Bild 2.1b.
Zur Lösung des Gleichungssystem in Bild 2.5müssen die geometrischen Randbedingungen, d. h. die fünf Auflagerbedingungen, berücksichtigt werden. Wegen 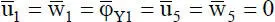 entfallen die Spalten 1 bis 3 sowie 13 und 14. Dies gilt auch für die entsprechenden Zeilen, da sie zu
entfallen die Spalten 1 bis 3 sowie 13 und 14. Dies gilt auch für die entsprechenden Zeilen, da sie zu 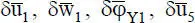 und
und 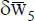 gehören und zudem der Lastvektor an diesen Stellen die unbekannten Auflagerreaktionen enthält. In Bild 2.5ist das Streichen der Spalten und Zeilen durch die horizontalen und vertikalen Pfeilpaare auf der Hauptdiagonalen anschaulich dargestellt. Es verbleibt ein 10×10-Gleichungssystem, das gemäß Abschnitt 3.6gelöst werden kann. Als Ergebnis erhält man die zehn vorher unbekannten Verformungsgrößen im Vektor
gehören und zudem der Lastvektor an diesen Stellen die unbekannten Auflagerreaktionen enthält. In Bild 2.5ist das Streichen der Spalten und Zeilen durch die horizontalen und vertikalen Pfeilpaare auf der Hauptdiagonalen anschaulich dargestellt. Es verbleibt ein 10×10-Gleichungssystem, das gemäß Abschnitt 3.6gelöst werden kann. Als Ergebnis erhält man die zehn vorher unbekannten Verformungsgrößen im Vektor 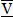 .
.
Die Berechnung der Auflagerreaktionen ist aus Bild 2.5unmittelbar ersichtlich, da die Zeilen 1 bis 3 sowie 13 und 14 diese Größen enthalten und nun alle Verformungsgrößen im Vektor 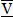 bekannt sind. Die Ermittlung der Schnittgrößen ist dagegen etwas aufwändiger, da dabei die einzelnen Stabelemente mit ihren lokalen x-z-KOS zu betrachten sind. Die Berechnung erfolgt mithilfe von Gl. (2.2), wobei jedoch die lokalen Verschiebungsgrößen im Vektor
bekannt sind. Die Ermittlung der Schnittgrößen ist dagegen etwas aufwändiger, da dabei die einzelnen Stabelemente mit ihren lokalen x-z-KOS zu betrachten sind. Die Berechnung erfolgt mithilfe von Gl. (2.2), wobei jedoch die lokalen Verschiebungsgrößen im Vektor 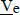 für jedes Stabelement ermittelt werden müssen. Dazu wird der Vektor
für jedes Stabelement ermittelt werden müssen. Dazu wird der Vektor 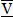 des Systems verwendet, die benötigten Größen den Elementknoten zugeordnet und in das lokale KOS transformiert. Einzelheiten können Abschnitt 3.7entnommen werden.
des Systems verwendet, die benötigten Größen den Elementknoten zugeordnet und in das lokale KOS transformiert. Einzelheiten können Abschnitt 3.7entnommen werden.
2.3 Ablauf der Berechnungen
Die Vorgehensweise bei der FEM unter Verwendung des Weggrößenverfahrens ist für die lineare Theorie in Tabelle 2.1zusammengestellt. Es spielt dabei keine Rolle, ob es sich um Stab-, Scheiben-, Platten- oder Schalenelemente handelt, mit denen das baustatische System diskretisiert wird. Unabhängig von den verwendeten Elementtypen ergibt sich stets der gleiche Ablauf für die Berechnungen, so dass mit ein und derselben Methodik zahlreiche Aufgabenstellungen gelöst werden können. Ein weiterer Vorteil ist die stark schematische Vorgehensweise, die keine individuellen Entscheidungen erfordert, da lediglich geeignete finite Elemente und eine sinnvolle Elementierung gewählt werden müssen.
In Tabelle 2.1wird davon ausgegangen, dass unter Punkt 2 alleElementsteifigkeitsmatrizen berechnet und abgespeichert werden, da sie unter Punkt 9 erneut zur Schnittgrößenermittlung benötigt werden, und dass sie erst unter Punkt 4 nach Abschluss von Punkt 2 eingeordnet werden. Diese Darstellungsweise ist für das Verständnis vorteilhaft, entspricht aber nicht dem üblichen Vorgehen. In der Regel werden die einzelnen Elementsteifigkeitsmatrizen berechnet und unmittelbar ohne Speicherung in die Gesamtsteifigkeit eingeordnet. Für die Schnittgrößenermittlung gemäß Punkt 9 werden sie dann erneutberechnet. Der hier beschriebene Ablauf für die Elementsteifigkeitsmatrizen wird in analoger Weise auch bei den elementbezogenen Lastgrößen verwendet, s. Punkte 3, 5 und 9.
Tabelle 2.1 Vorgehensweise beim Weggrößenverfahren (lineare Theorie)
| Nr. |
Tätigkeit |
Einzelheiten |
| 1 |
Baustatisches System in Elemente aufteilen |
Bild 2.1b |
| 2 |
Für jedes Element:Elementsteifigkeitsmatrix berechnen |
Abschn. 3.2 |
| 3 |
Für jedes Element:Belastungen, die innerhalb der Elemente wirken, in äquivalente Knotenlasten umrechnen (Elementlastvektor) |
Abschn. 3.2 |
| 4 |
Elementsteifigkeitsmatrizen transformieren und in die Gesamtsteifigkeitsmatrix einordnen |
Abschn. 3.4, Bild 2.4 Abschn. 3.5.2, Bild 2.5 |
| 5 |
In den Knoten angreifende Lastgrößen und Knotenlasten gemäß Punkt 3 in den Gesamtlastvektor des Systems einordnen |
Abschn. 3.5.3, Bild 2.5 |
| 6 |
Gegebenenfalls Federn, Schubfelder und Gelenke berücksichtigen |
Abschn. 3.10, 3.11, Bild 2.5 |
| 7 |
Geometrische Randbedingungen (Auflager, Einspannungen, usw.) in der Gesamtsteifigkeitsmatrix und im Gesamtlastvektor berücksichtigen |
Abschn. 3.5.4 |
| 8 |
Als Ergebnis der Punkte 4 bis 7 ergibt sich das Gleichungssystem: 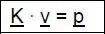 Durch Lösen des Gleichungssystems erhält man die Verformungen des Systems in den Knoten. Durch Lösen des Gleichungssystems erhält man die Verformungen des Systems in den Knoten. |
Abschn. 3.6 Kapitel 8 |
| 9 |
Für jedes Element: Berechnung der Schnittgrößen in den Knoten mit den Elementsteifigkeitsbeziehungen (Steifigkeitsmatrizen gemäß Pkt. 2 und Lastvektoren gemäß Pkt. 3) und den nunmehr bekannten Knotenverformungen (s. Pkt. 8) |
Abschn. 3.7 |
| 10 |
Für jedes Element: Gegebenenfalls Berechnung der Schnittgrößen im Elementinneren mithilfe der Formfunktionen |
Abschn. 3.7 |
Für Berechnungen nach Theorie II. Ordnungwird ebenfalls gemäß Tabelle 2.1vorgegangen und das System zunächst nach Theorie I. Ordnung analysiert (1. Durchlauf). Anschließend wird nochmals bei Punkt 2 begonnenund es werden nun zusätzlich geometrische Elementsteifigkeitsmatrizenberechnet, für die die Schnittgrößen aus Punkt 9 der 1. Berechnung, also nach Theorie I. Ordnung, benötigt werden. In diesem 2. Durchlauf wird unter Punkt 4 zusätzlich eine geometrische Gesamtsteifigkeitsmatrix erzeugt, so dass die Matrix des Gleichungssystems gemäß Punkt 8 nun aus zwei Matrizen
(2.6) 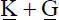
besteht. Die Matrix 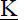 gehört zur linearen Theorie und repräsentiert die Steifigkeit des Systems.
gehört zur linearen Theorie und repräsentiert die Steifigkeit des Systems.  enthält die Zusatzanteile für Theorie II. Ordnung. Auf die Berücksichtigung von Vorverformungen bzw. geometrischer Ersatzimperfektionen wird in Abschnitt 4.7und auf die Berechnung der Schnittgrößen in Abschnitt 4.8ausführlich eingegangen.
enthält die Zusatzanteile für Theorie II. Ordnung. Auf die Berücksichtigung von Vorverformungen bzw. geometrischer Ersatzimperfektionen wird in Abschnitt 4.7und auf die Berechnung der Schnittgrößen in Abschnitt 4.8ausführlich eingegangen.
Читать дальше

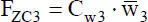
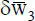 , so dass zu dem Hauptdiagonalelement in der 8. Zeile der Wert von C w3hinzu zu addieren ist.
, so dass zu dem Hauptdiagonalelement in der 8. Zeile der Wert von C w3hinzu zu addieren ist.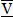 enthält die 15 Verschiebungsgrößen in den fünf Knoten, die in Bild 2.1ddargestellt sind. Im Gesamtlastvektor
enthält die 15 Verschiebungsgrößen in den fünf Knoten, die in Bild 2.1ddargestellt sind. Im Gesamtlastvektor 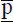 sind die Lastgrößen und die Auflagerreaktionen zusammengestellt. Dabei beziehen sich die Vorzeichen, wie bereits er-wähnt, auf das globale X-Z-KOS in Bild 2.1b.
sind die Lastgrößen und die Auflagerreaktionen zusammengestellt. Dabei beziehen sich die Vorzeichen, wie bereits er-wähnt, auf das globale X-Z-KOS in Bild 2.1b.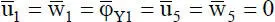 entfallen die Spalten 1 bis 3 sowie 13 und 14. Dies gilt auch für die entsprechenden Zeilen, da sie zu
entfallen die Spalten 1 bis 3 sowie 13 und 14. Dies gilt auch für die entsprechenden Zeilen, da sie zu 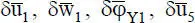 und
und 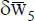 gehören und zudem der Lastvektor an diesen Stellen die unbekannten Auflagerreaktionen enthält. In Bild 2.5ist das Streichen der Spalten und Zeilen durch die horizontalen und vertikalen Pfeilpaare auf der Hauptdiagonalen anschaulich dargestellt. Es verbleibt ein 10×10-Gleichungssystem, das gemäß Abschnitt 3.6gelöst werden kann. Als Ergebnis erhält man die zehn vorher unbekannten Verformungsgrößen im Vektor
gehören und zudem der Lastvektor an diesen Stellen die unbekannten Auflagerreaktionen enthält. In Bild 2.5ist das Streichen der Spalten und Zeilen durch die horizontalen und vertikalen Pfeilpaare auf der Hauptdiagonalen anschaulich dargestellt. Es verbleibt ein 10×10-Gleichungssystem, das gemäß Abschnitt 3.6gelöst werden kann. Als Ergebnis erhält man die zehn vorher unbekannten Verformungsgrößen im Vektor 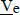 für jedes Stabelement ermittelt werden müssen. Dazu wird der Vektor
für jedes Stabelement ermittelt werden müssen. Dazu wird der Vektor 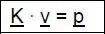 Durch Lösen des Gleichungssystems erhält man die Verformungen des Systems in den Knoten.
Durch Lösen des Gleichungssystems erhält man die Verformungen des Systems in den Knoten.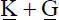
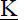 gehört zur linearen Theorie und repräsentiert die Steifigkeit des Systems.
gehört zur linearen Theorie und repräsentiert die Steifigkeit des Systems.  enthält die Zusatzanteile für Theorie II. Ordnung. Auf die Berücksichtigung von Vorverformungen bzw. geometrischer Ersatzimperfektionen wird in Abschnitt 4.7und auf die Berechnung der Schnittgrößen in Abschnitt 4.8ausführlich eingegangen.
enthält die Zusatzanteile für Theorie II. Ordnung. Auf die Berücksichtigung von Vorverformungen bzw. geometrischer Ersatzimperfektionen wird in Abschnitt 4.7und auf die Berechnung der Schnittgrößen in Abschnitt 4.8ausführlich eingegangen.










