Ein nächster wichtiger Punkt beim Weggrößenverfahren ist die Definition der Verschiebungsgrößen, siehe Bild 2.1d. In jedem Knoten treten die drei Größen 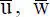 und
und 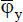 auf, die zu den Lastgrößen F X, F Zund M YLunmittelbar korrespondieren. Da später auch lokale Verschiebungsgrößen benötigt werden, erfolgt die Kennzeichnung der globalen Größen mit einem Querstrich. Wie man sieht, treten 5 ⋅ 3 = 15 unbekannte Verschiebungsgrößen ( Knotenfreiwerte ) auf. Aufgrund der geometrischen Randbedingungen(Auflagerbedingungen: Einspannung links und gelenkiges Auflager rechts) sind fünf Knotenfreiwerte gleich null, und es verbleiben zehn unbekannte Freiwerte, die zu berechnen sind. Es sei hier angemerkt, dass die Auflagerkräfte am gelenkigen Auflager durch die horizontalen und vertikalen Komponenten ersetzt worden sind.
auf, die zu den Lastgrößen F X, F Zund M YLunmittelbar korrespondieren. Da später auch lokale Verschiebungsgrößen benötigt werden, erfolgt die Kennzeichnung der globalen Größen mit einem Querstrich. Wie man sieht, treten 5 ⋅ 3 = 15 unbekannte Verschiebungsgrößen ( Knotenfreiwerte ) auf. Aufgrund der geometrischen Randbedingungen(Auflagerbedingungen: Einspannung links und gelenkiges Auflager rechts) sind fünf Knotenfreiwerte gleich null, und es verbleiben zehn unbekannte Freiwerte, die zu berechnen sind. Es sei hier angemerkt, dass die Auflagerkräfte am gelenkigen Auflager durch die horizontalen und vertikalen Komponenten ersetzt worden sind.
Eine weitere wesentliche Grundideeder FEM besteht darin, die Knoten eines Tragwerks freizuschneiden und an den Knoten mithilfe des Prinzips der virtuellen Verrückungen bzw. der virtuellen Arbeitdas Gleichgewicht zu formulieren:
(2.1) 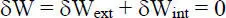
Das Prinzip wird in Abschnitt 2.4.2erläutert. Beispielhaft wird in Bild 2.2der Knoten 4 des ebenen Rahmens betrachtet. Die Einzellastgrößen führen zur äußeren virtuellen Arbeit δW ext, die Knotenschnittgrößen der angrenzenden Stabelemente zur inneren virtuellen Arbeit δW int. Dabei ist zu beachten, dass sich die Knotenschnittgrößen mit Querstrich ebenso wie die Lastgrößen auf das globale X-Z-KOS beziehen und sich entsprechend die virtuelle Arbeit mit den globalen Knotenverformungsgrößen ergibt. Die Richtungen bzw. Vorzeichen der Knotenschnittgrößen ergeben sich aus dem Gleichgewicht mit den Stabendschnittgrößen(Richtung wie die Lastgrößen!), die übrigens an beidenElementenden mit den angegebenen Richtungen positiv definiert sind. Die daraus resultierende Vorzeichendefinition IIfür die Stabendschnittgrößen ist ein wesentlicher Bestandteil der FEM und der systematischen Bildung des Knotengleichgewichts.
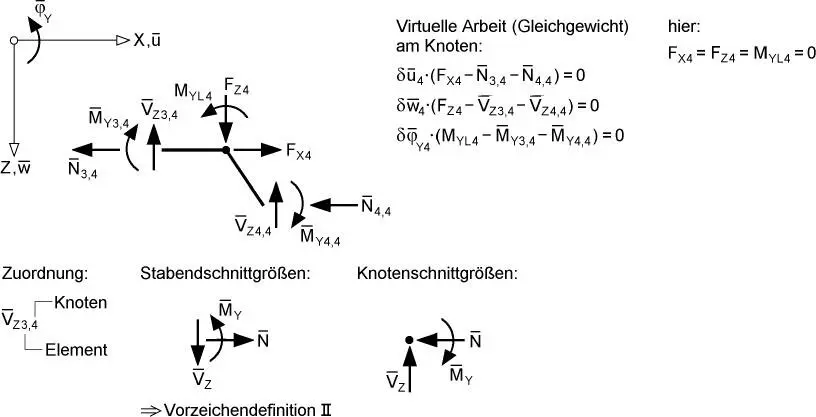
Bild 2.2 Gleichgewicht am Knoten 4
Betrachtet man die aus den virtuellen Verrückungen 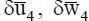 und
und 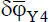 entstehenden virtuellen Arbeiten getrennt voneinander, so ergeben sich drei Gleichgewichtsbedingungen, die in Bild 2.2angegeben werden. Die Ausdrücke in den runden Klammern müssen gleich null sein. Dies entspricht den Bedingungen des „klassischen“ Knotengleichgewichts für Σ F X= 0, Σ F Z= 0 und Σ M Y= 0.
entstehenden virtuellen Arbeiten getrennt voneinander, so ergeben sich drei Gleichgewichtsbedingungen, die in Bild 2.2angegeben werden. Die Ausdrücke in den runden Klammern müssen gleich null sein. Dies entspricht den Bedingungen des „klassischen“ Knotengleichgewichts für Σ F X= 0, Σ F Z= 0 und Σ M Y= 0.
Da man das Gleichgewicht in analoger Weise an jedem Knoten eines Tragwerks bilden kann, erhält man für den ebenen Rahmen mit fünf Knoten in Bild 2.1insgesamt 15 Bedingungen, durch die das Gleichgewicht des Rahmens erfasst wird. Die Forderung, dass an jedemKnoten eines Tragwerks die virtuelle Arbeit gleich null sein muss, ist ein zentraler Bestandteil der FEM.
Die Bedingungen für das Gleichgewicht an den Knoten reichen nicht aus, um die unbekannten Knotenschnittgrößen bestimmen zu können. Beispielsweise enthalten die 15 Gleichungen für den ebenen Rahmen mehr als 15 unbekannte Knotenschnittgrößen. Zur Lösung des Problems benötigt man daher eine weitere Grundidee. Dazu werden in Bild 2.3ebenfalls beispielhaft das Stabelement4 betrachtet und sechs Beziehungen zwischen den lokalen Stabendschnittgrößen und den korrespondierenden Verformungsgrößen aufgestellt. Ihre Herleitung auf Grundlage der virtuellen Arbeit gehört zum Kern der FEM und des Weggrößenverfahrens und wird in Abschnitt 3.2für Stabelemente ausführlich behandelt. In Matrizenschreibweise lautet die Elementsteifigkeitsbeziehung unter Berücksichtigung der „Elementlasten“:
(2.2) 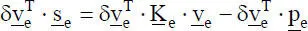
In Gl. (2.2)beziehen sich alle Größen auf das lokale x-z-KOS des Stabelementes. Die Transformation in das globale X-Z-KOS wird in Abschnitt 3.4ausführlich behandelt; als Ergebnis erhält man:
(2.3) 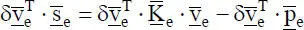
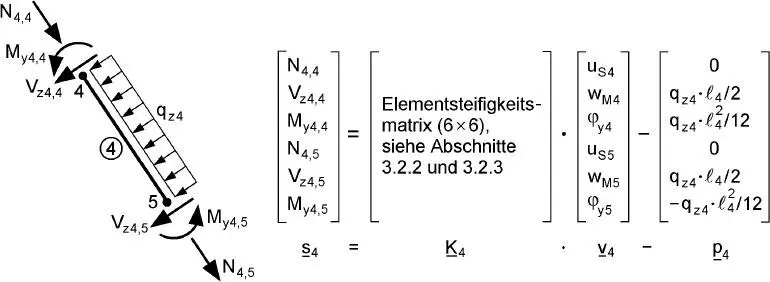
Bild 2.3 Stabendschnittgrößen von Element 4
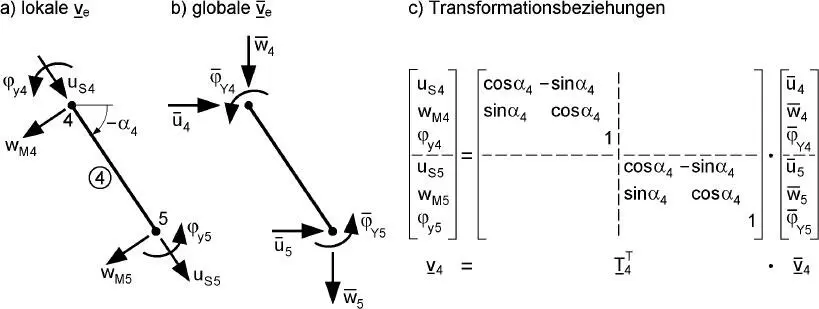
Bild 2.4 Transformation der lokalen Knotenverschiebungsgrößen von Stabelement 4 in das globale X-Z-Koordinatensystem
Eine anschauliche Interpretation von Gl. (2.3)gelingt mithilfe von Bild 2.4. Dort werden die lokalenKnotenverschiebungsgrößen von Stabelement 4 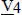 in das globale XZ-KOS transformiert, so dass sie durch die Größen im globalen System ersetzt werden können. Da dies in vergleichbarer Weise auch für die Schnittgrößen erfolgen kann (s. Abschnitt 3.4.1), ist es nun möglich, die Schnittgrößen in den Bedingungen für das Knotengleichgewicht zu ersetzen. Diese Vorgehensweise ist anschaulich erkennbar, wenn man beispielsweise die Knotenschnittgrößen am Knoten 4 von Element 4 in Bild 2.2betrachtet, mit den Stabendschnittgrößen in Bild 2.3vergleicht und Transformationen wie in Bild 2.4durchführt. Als Ergebnis können die Gleichgewichtsbedingungen an allen Knoten zu einem Gleichungssystem zusammengefasst werden, s. Bild 2.5:
in das globale XZ-KOS transformiert, so dass sie durch die Größen im globalen System ersetzt werden können. Da dies in vergleichbarer Weise auch für die Schnittgrößen erfolgen kann (s. Abschnitt 3.4.1), ist es nun möglich, die Schnittgrößen in den Bedingungen für das Knotengleichgewicht zu ersetzen. Diese Vorgehensweise ist anschaulich erkennbar, wenn man beispielsweise die Knotenschnittgrößen am Knoten 4 von Element 4 in Bild 2.2betrachtet, mit den Stabendschnittgrößen in Bild 2.3vergleicht und Transformationen wie in Bild 2.4durchführt. Als Ergebnis können die Gleichgewichtsbedingungen an allen Knoten zu einem Gleichungssystem zusammengefasst werden, s. Bild 2.5:
(2.4) 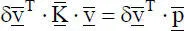
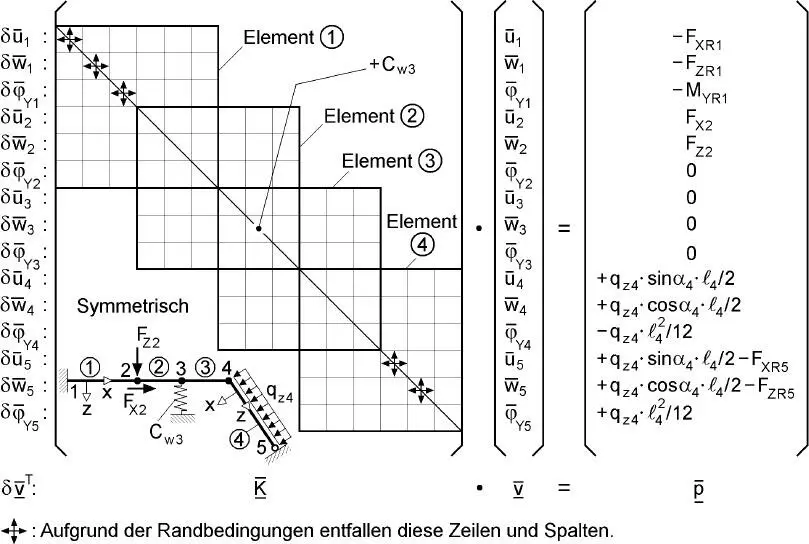
Bild 2.5 Gleichungssystem für den ebenen Rahmen in Bild 2.1
Für den ebenen Rahmen in Bild 2.1aerhält man das in Bild 2.5dargestellte Gleichungssystem, das aus 15 einzelnen Gleichungen besteht, die den auf der linken Seite aufgeführten virtuellen Verschiebungsgrößenzugeordnet und in Matrizenschreibweise zusammengefasst sind. Die Gesamtsteifigkeitsmatrix 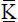 enthält dabei die vier Stabelemente, die durch die 6×6-Elementmatrizen gekennzeichnet sind. Wie man sieht, ergibt sich eine Überlappung der Elementmatrizen an den gemeinsamen Knoten (Verbindungsknoten), so dass in diesen Bereichen ihre Werte aufaddiert werden. Die PunktfederC w3im Knoten 3 ist ebenfalls in der Gesamtsteifigkeitsmatrix zu berücksichtigen. Die Federkraft F ZC3wirkt entgegengesetzt zur Auflagerreaktion F ZR3in Bild 2.1cund kann durch
enthält dabei die vier Stabelemente, die durch die 6×6-Elementmatrizen gekennzeichnet sind. Wie man sieht, ergibt sich eine Überlappung der Elementmatrizen an den gemeinsamen Knoten (Verbindungsknoten), so dass in diesen Bereichen ihre Werte aufaddiert werden. Die PunktfederC w3im Knoten 3 ist ebenfalls in der Gesamtsteifigkeitsmatrix zu berücksichtigen. Die Federkraft F ZC3wirkt entgegengesetzt zur Auflagerreaktion F ZR3in Bild 2.1cund kann durch
Читать дальше

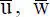 und
und 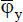 auf, die zu den Lastgrößen F X, F Zund M YLunmittelbar korrespondieren. Da später auch lokale Verschiebungsgrößen benötigt werden, erfolgt die Kennzeichnung der globalen Größen mit einem Querstrich. Wie man sieht, treten 5 ⋅ 3 = 15 unbekannte Verschiebungsgrößen ( Knotenfreiwerte ) auf. Aufgrund der geometrischen Randbedingungen(Auflagerbedingungen: Einspannung links und gelenkiges Auflager rechts) sind fünf Knotenfreiwerte gleich null, und es verbleiben zehn unbekannte Freiwerte, die zu berechnen sind. Es sei hier angemerkt, dass die Auflagerkräfte am gelenkigen Auflager durch die horizontalen und vertikalen Komponenten ersetzt worden sind.
auf, die zu den Lastgrößen F X, F Zund M YLunmittelbar korrespondieren. Da später auch lokale Verschiebungsgrößen benötigt werden, erfolgt die Kennzeichnung der globalen Größen mit einem Querstrich. Wie man sieht, treten 5 ⋅ 3 = 15 unbekannte Verschiebungsgrößen ( Knotenfreiwerte ) auf. Aufgrund der geometrischen Randbedingungen(Auflagerbedingungen: Einspannung links und gelenkiges Auflager rechts) sind fünf Knotenfreiwerte gleich null, und es verbleiben zehn unbekannte Freiwerte, die zu berechnen sind. Es sei hier angemerkt, dass die Auflagerkräfte am gelenkigen Auflager durch die horizontalen und vertikalen Komponenten ersetzt worden sind.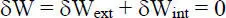

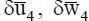 und
und 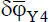 entstehenden virtuellen Arbeiten getrennt voneinander, so ergeben sich drei Gleichgewichtsbedingungen, die in Bild 2.2angegeben werden. Die Ausdrücke in den runden Klammern müssen gleich null sein. Dies entspricht den Bedingungen des „klassischen“ Knotengleichgewichts für Σ F X= 0, Σ F Z= 0 und Σ M Y= 0.
entstehenden virtuellen Arbeiten getrennt voneinander, so ergeben sich drei Gleichgewichtsbedingungen, die in Bild 2.2angegeben werden. Die Ausdrücke in den runden Klammern müssen gleich null sein. Dies entspricht den Bedingungen des „klassischen“ Knotengleichgewichts für Σ F X= 0, Σ F Z= 0 und Σ M Y= 0.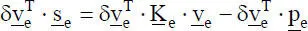
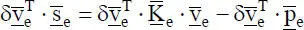


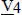 in das globale XZ-KOS transformiert, so dass sie durch die Größen im globalen System ersetzt werden können. Da dies in vergleichbarer Weise auch für die Schnittgrößen erfolgen kann (s. Abschnitt 3.4.1), ist es nun möglich, die Schnittgrößen in den Bedingungen für das Knotengleichgewicht zu ersetzen. Diese Vorgehensweise ist anschaulich erkennbar, wenn man beispielsweise die Knotenschnittgrößen am Knoten 4 von Element 4 in Bild 2.2betrachtet, mit den Stabendschnittgrößen in Bild 2.3vergleicht und Transformationen wie in Bild 2.4durchführt. Als Ergebnis können die Gleichgewichtsbedingungen an allen Knoten zu einem Gleichungssystem zusammengefasst werden, s. Bild 2.5:
in das globale XZ-KOS transformiert, so dass sie durch die Größen im globalen System ersetzt werden können. Da dies in vergleichbarer Weise auch für die Schnittgrößen erfolgen kann (s. Abschnitt 3.4.1), ist es nun möglich, die Schnittgrößen in den Bedingungen für das Knotengleichgewicht zu ersetzen. Diese Vorgehensweise ist anschaulich erkennbar, wenn man beispielsweise die Knotenschnittgrößen am Knoten 4 von Element 4 in Bild 2.2betrachtet, mit den Stabendschnittgrößen in Bild 2.3vergleicht und Transformationen wie in Bild 2.4durchführt. Als Ergebnis können die Gleichgewichtsbedingungen an allen Knoten zu einem Gleichungssystem zusammengefasst werden, s. Bild 2.5: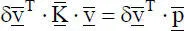

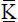 enthält dabei die vier Stabelemente, die durch die 6×6-Elementmatrizen gekennzeichnet sind. Wie man sieht, ergibt sich eine Überlappung der Elementmatrizen an den gemeinsamen Knoten (Verbindungsknoten), so dass in diesen Bereichen ihre Werte aufaddiert werden. Die PunktfederC w3im Knoten 3 ist ebenfalls in der Gesamtsteifigkeitsmatrix zu berücksichtigen. Die Federkraft F ZC3wirkt entgegengesetzt zur Auflagerreaktion F ZR3in Bild 2.1cund kann durch
enthält dabei die vier Stabelemente, die durch die 6×6-Elementmatrizen gekennzeichnet sind. Wie man sieht, ergibt sich eine Überlappung der Elementmatrizen an den gemeinsamen Knoten (Verbindungsknoten), so dass in diesen Bereichen ihre Werte aufaddiert werden. Die PunktfederC w3im Knoten 3 ist ebenfalls in der Gesamtsteifigkeitsmatrix zu berücksichtigen. Die Federkraft F ZC3wirkt entgegengesetzt zur Auflagerreaktion F ZR3in Bild 2.1cund kann durch










