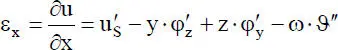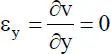1 ...7 8 9 11 12 13 ...23 Querschnittskennwerte
| A |
Fläche |
| I y, I z |
Hauptträgheitsmomente |
| I ω |
Wölbwiderstand, DIN EN 1993: I w |
| I T |
Torsionsträgheitsmoment |
| W y, W z |
Widerstandsmomente |
| S y, S z |
statische Momente |
| i M, r y, r z, r ω |
Größen für Theorie II. Ordnung und Stabilität, s. Tabelle 4.1 |
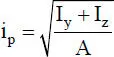 |
polarer Trägheitsradius |
Biegeknicken und Biegedrillknicken
| N cr |
ideale Drucknormalkraft (Elastizitätstheorie, Eigenwert) |
| L cr |
Knicklänge für Biegeknicken |
| ε |
Stabkennzahl für Biegeknicken |
| α cr |
Verzweigungslastfaktor des Systems (Eigenwert) |
| M cr,y |
ideales Biegedrillknickmoment (Elastizitätstheorie, Eigenwert) |
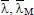 |
bezogene Schlankheitsgrade |
| χ, χ LT |
Abminderungsfaktoren (LT: Lateral Torsional Buckling |
Weitere Bezeichnungen und Annahmen
Werkstoffkennwerte (isotroper Werkstoff) und Teilsicherheitsbeiwerte
| E |
Elastizitätsmodul |
E = 21000 kN/cm 2 |
| G |
Schubmodul |
G = E/(2·(1 + ν)) ≈ 8100 kN/cm ² |
| ν |
Querdehnzahl, Poissonsche Zahl |
ν = 0,3 |
| α |
Wärmeausdehnungskoeffizient |
α = 12.10 −6je K (für T ≤ 100 °C) |
| ρ |
Dichte |
ρ = 7850 kg/m 3 |
Die als Bemessungswerte angegebenen Materialkonstanten sind in der Regel für Berechnungen anzunehmen.
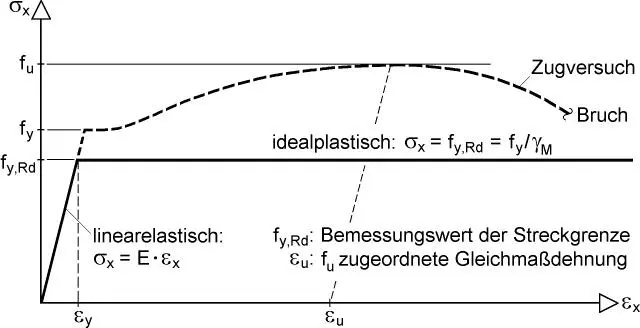
Bild 1.11 Spannungs-Dehnungs-Beziehung für Baustahl
| f y |
Streckgrenze |
| f u |
Zugfestigkeit |
| ε u |
Gleichmaßdehnung |
| ε ult |
Bruchdehnung |
| γ M |
Beiwert für die Widerstandsgrößen ( Material) |
| γ F |
Beiwert für die Einwirkungen ( Force) |
Die Bezeichnungen f y, f u, ε uund γ Mwerden in Bild 1.11anhand der Spannungs-Dehnungs-Beziehung für Baustahl erläutert. Bei Stabilitätsnachweisen in Form von Querschnittsnachweisen mit Schnittgrößen nach Theorie II. Ordnung ist bei der Ermittlung der Beanspruchbarkeit von Querschnitten der Wert γ M= 1,1 anzusetzen, s. auch Abschnitt 5.1.2.
Matrizen und Vektoren
| s |
Schnittgrößenvektor |
| K |
Steifigkeitsmatrix |
| G |
geometrische Steifigkeitsmatrix |
| v |
Verformungsgrößenvektor |
| p |
Lastgrößenvektor |
| Index e: |
Element |
Ein Querstrich über den Matrizen und Vektoren weist daraufhin, dass sie für das globale Koordinatensystem (X, Y, Z) gelten.
Annahmen und Voraussetzungen
Sofern nicht anders angegeben, gelten folgende Annahmen und Voraussetzungen:
Sofern nicht anders angegeben, gelten folgende Annahmen und Voraussetzungen:
• Es wird ein linearelastisches-idealplastisches Werkstoffverhalten gemäß Bild 1.11vorausgesetzt.
• Auftretende Verformungen sind im Sinne der Stabtheorie klein, so dass geometrische Beziehungen linearisiert werden können.
• Die Querschnittsform eines Stabes bleibt bei Belastung und Verformung erhalten.
• Für zweiachsige Biegung mit Normalkraft werden die Bernoulli-Hypothese vom Ebenbleiben der Querschnitte vorausgesetzt und der Einfluss von Schubspannungen infolge von Querkräften auf die Verformungen vernachlässigt (schubstarre Stäbe).
• Bei der Wölbkrafttorsion werden die Wagner-Hypothese vorausgesetzt und der Einfluss von Schubspannungen infolge des sekundären Torsionsmomentes auf die Verdrehung vernachlässigt.
1.6 Grundlegende Beziehungen
Verschiebungen (lineare Stabtheorie)
Wie bei Stäben allgemein üblich sind y und z die Hauptachsen des Querschnitts und ω ist die normierte Wölbordinate, [12]. Die Längsverschiebung u Sbezieht sich auf den Schwerpunkt S und die Verschiebungen v Msowie w Mbeschreiben die Verschiebung des Schubmittelpunktes M. Für die Stablängsverschiebung u eines beliebigen Querschnittspunktes gilt folgende Beziehung:
(1.1) 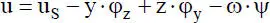
Der erste Anteil ist die Verschiebung infolge einer Normalkraftbeanspruchung, der zweite und dritte resultiert aus den Biegemomenten und stellt die Verschiebung aufgrund von Querschnittsverdrehungen φ yund φ zdar. Dabei können mit Gl. (1.1)nur Verschiebungen erfasst werden, bei denen der Querschnitt eben bleibt. Der vierte Anteil erfasst die Stablängsverschiebung aus Torsionsbeanspruchungen in Abhängigkeit von der Verdrillung ψ. Bild 1.12veranschaulicht die mit Gl. (1.1)verbundenen Verformungen u des Querschnitts für positive Größen φ y, φ zund ψ.
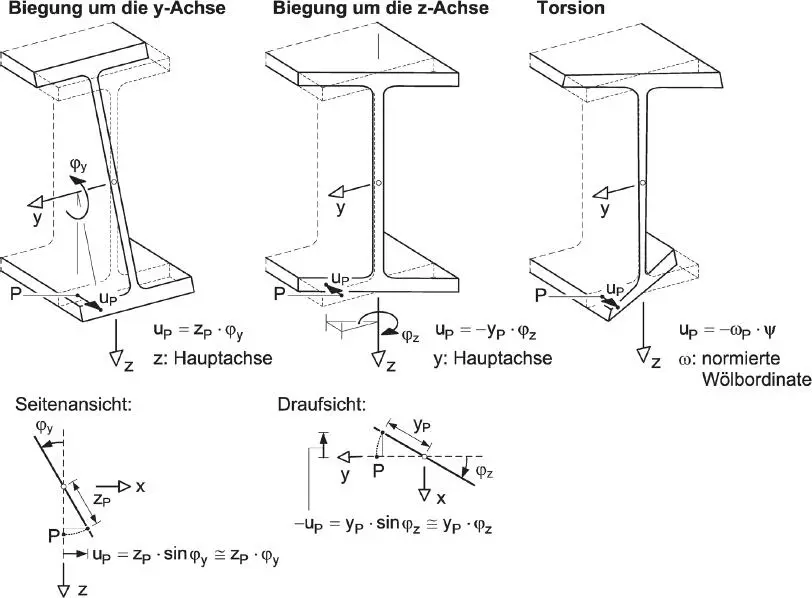
Bild 1.12 Längsverschiebung u eines Punktes P infolge zweiachsiger Biegung und Torsion
Die Verformungen v und w in der Querschnittsebene ergeben sich aus der Verschiebung des Schubmittelpunktes M sowie aus zusätzlichen Verschiebungsanteilen, die aus der Verdrehung ϑ resultieren, s. Bild 1.13:
(1.2) 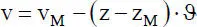
(1.3) 
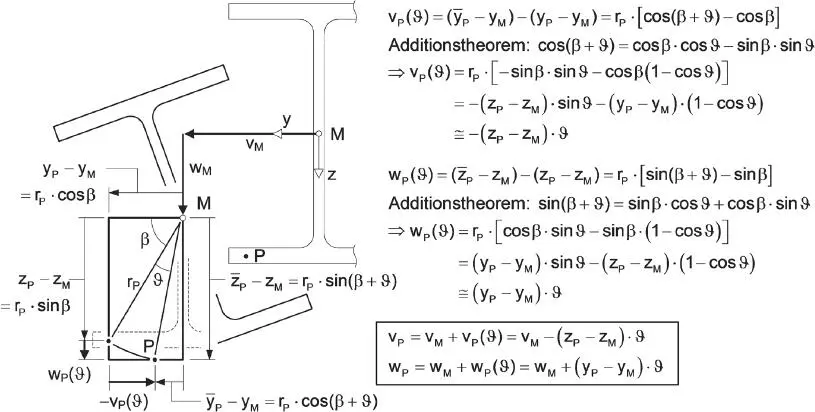
Bild 1.13 Verschiebungen v und w eines Punktes P
Verzerrungen (lineare Stabtheorie)
Die Verzerrungen werden durch geometrische Beziehungen mit den Verschiebungsgrößen verknüpft. Nach [12] gelten für die lineare Stabtheorie die nachstehenden Beziehungen, wobei für die Verschiebungen die Gln. (1.1)bis (1.3)berücksichtigt werden. Außerdem gilt wegen der Vernachlässigung sekundärer Schubverformungen 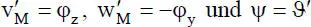 .
.
(1.4a) 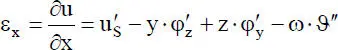
(1.4b) 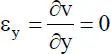
Читать дальше

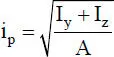
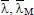

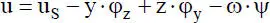

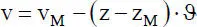


 .
.