Matthias Krauß - Finite-Elemente-Methoden im Stahlbau

• einfeldrige und durchlaufende Biegeträger

• Stützen und ebene Rahmen

• ebene und räumliche Fachwerke

• räumliche Stabtragwerke

• Trägerroste

Die hier aufgeführten baustatischen Systeme kommen vornehmlich im Hoch-, Industrie- und Anlagenbauvor. Sie erfordern aufgrund unterschiedlicher Beanspruchungen Stabelemente mit bis zu sieben Verformungsgrößen in den Knoten (Knotenfreiwerte). Auf die Anzahl der erforderlichen Verformungsgrößen pro Knoten wird in den Kapiteln 3und 5näher eingegangen.

Stabelementesind auch für die Berechnung von Brückendie üblichen finiten Elemente. Ob Vollwandträger-, Fachwerkbalken-, Stabbogen- oder Schrägseilbrücken, Flächenelemente (Scheiben, Platten, Schalen) werden nur selten verwendet. Ein wesentlicher Hintergrund dazu ist, dass die aktuellen Vorschriften fast ausschließlich auf die Berechnung mit Stabtragwerken abgestimmt sind. Hinzu kommt, dass die Genauigkeit dieser Berechnungen von Ausnahmen abgesehen völlig ausreichend ist.

Ein durchaus interessanter Anwendungsbereich von finiten Flächenelementenim Stahlbau ist das Plattenbeulen. Bild 1.3bzeigt beispielhaft den Obergurt eines Stabes, der für die Untersuchung des Plattenbeulens in finite Elemente eingeteilt worden ist. Das Thema wird in Kapitel 5behandelt und dort ein rechteckiges Plattenelement für die Berechnung von Eigenwerten und Eigenformen hergeleitet. Ansonsten werden Flächenelemente bei wissenschaftlichen Untersuchungen und Entwicklungen gezielt eingesetzt. Da, wie erwähnt, Flächenelemente nur selten und Volumenelemente praktisch gar nicht im Stahlbau zum Einsatz kommen, soll hier zusammenfassend Folgendes festgehalten werden:

• Tragwerke des Stahlbaus werden fast ausschließlich mithilfe von Stabelementen berechnet.

• Es werden unterschiedliche Stabelemente benötigt, damit alle vorkommenden Tragwerks- und Beanspruchungsarten zutreffend untersucht werden können.

Finite Elemente für die Untersuchung von Stabquerschnittenwerden in Kapitel 7behandelt. Als Beispiel dazu ist in Bild 1.3cdie FE-Modellierung eines gewalzten I-Querschnitts durch krummlinig berandete Flächenelemente dargestellt.

Lineare Berechnungen (Theorie I. Ordnung) bilden in der Regel gedanklich und rechnerisch den Ausgangspunkt. Grundlage sind dabei folgende Annahmen:

• Der Werkstoff verhält sich im gesamten Tragwerk linearelastisch, d. h., es gilt uneingeschränkt das Hookesche Gesetz.

• Der Einfluss von Tragwerksverformungen ist so gering, dass sie vernachlässigt werden können und die Gleichgewichtsbeziehungen am unverformten System formuliert werden dürfen.

• Strukturelle und geometrische Imperfektionen, d. h. Eigenspannungen, Vorkrümmungen und Vorverdrehungen, können vernachlässigt werden.

Nichtlineare Berechnungen erfordern in der Regel einen höheren Aufwand als lineare. Man unterscheidet physikalische und geometrische Nichtlinearitäten. Bei der physikalischen Nichtlinearitätwird die Annahme „linearelastisches Werkstoffverhalten“ aufgegeben und das Plastizieren von Tragwerksteilen berücksichtigt, weil dann wirtschaftlichere, d. h. leichtere Konstruktionen ausgeführt werden können. Sofern das Plastizieren nur bei der Tragfähigkeit der Querschnitte ausgenutzt wird, ist diese Vorgehensweise der Nachweismethode 2in Tabelle 1.1zuzuordnen. Die Schnittgrößen werden nach der Elastizitätstheorie berechnet („elastische“ Tragwerksberechnung) und maximal ein Lastzustand zugelassen, bei dem sich einFließgelenk bildet. Im Gegensatz dazu werden bei der Nachweismethode 3plastische Tragfähigkeiten der Querschnitte und des Systems ausgenutzt, d. h. es wird die Ausbreitung von Fließzonen oder die Ausbildung mehrerer Fließgelenke zugelassen.

Während das physikalisch nichtlineare Werkstoffverhalten überwiegend aus wirtschaftlichen Gründen berücksichtigt wird, muss die geometrische Nichtlinearitätbei stabilitätsgefährdeten Stahlkonstruktionen unter Sicherheitsaspekten unabdingbar erfasst werden. Relativ große Verformungen führen dabei zu größeren Schnittgrößen und höheren Beanspruchungen im Vergleich zu linearen Berechnungen, so dass entsprechende Nachweise zum Biegeknicken, Biegedrillknicken oder Plattenbeulen geführt werden müssen.

Tabelle 1.3 Unterschiede zwischen Theorie I. und II. Ordnung sowie der geometrisch nichtlinearen Theorie nach [31]

	Theorie I. Ordnung (geometrisch lineare Theorie)	Theorie II. Ordnung	Geometrisch nichtlineare Theorie
Gleichgewicht	am unverformten System	am schwach verformten System	am stark verformten System
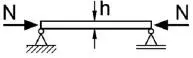
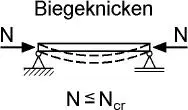
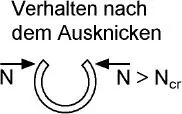
Stab unter Druckbelastung
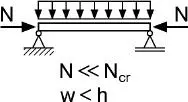
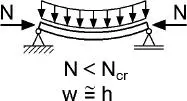
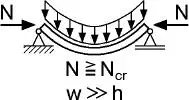
Stab unter Druck- und Querbelastung
Wirkliche Verzerrungen	Lineare kinematische Beziehungen	Nichtlineare kinematische Beziehungen
Virtuelle Verzerrungen	Aus linearen kinematischen Beziehungen	Aus nichtlinearen kinematischen Beziehungen - linearisiert - - nichtlinear -

Die Unterschiede zwischen der geometrisch linearen und nichtlinearen Theorie werden mithilfe von Tabelle 1.3erläutert. Bei der geometrisch nichtlinearen Theorie wird das Gleichgewicht am verformtenSystem formuliert und es werden dabei große Verformungen berücksichtigt. Mit dieser Theorie erhält man genaue Lösungen, die aber auch einen hohen Rechenaufwand erfordern. Mit der geometrisch nichtlinearen Theorie können sehr große Verformungen zutreffend berechnet und beschrieben werden, die jedoch im Zusammenhang mit Baukonstruktionen schon aus Gründen der Gebrauchstauglichkeit i. A. nicht auftreten und daher in der Regel ohne Bedeutung sind. Im Stahlbau wird daher eine „Theorie II. Ordnung“ eingesetzt, die eine Näherung der geometrisch nichtlinearen Theorie darstellt. Dabei werden das Gleichgewicht am verformtenSystem formuliert und aufgrund von Linearisierungen näherungsweise nur mäßige Verformungen berücksichtigt. Die Skizzen in Tabelle 1.3vermitteln anschaulich die Unterschiede bei den Verformungen. Darüber hinaus werden mit den letzten Zeilen Hinweise für theoretische Grundlagen gegeben. Sie beschreiben, wie die Verzerrungen bestimmt werden, wobei Spannungen mit den „wirklichen Verzerrungen“ ermittelt werden und die „virtuellen Verzerrungen“ zur Formulierung der virtuellen Arbeit in den Abschnitten 2.4.2und 4.3dienen. Die Zusammenhänge zwischen linearen, linearisierten und nichtlinearen Beziehungen werden in Abschnitt 1.7veranschaulicht.