1 ...6 7 8 10 11 12 ...23 Im Zusammenhang mit geometrisch nichtlinearen Berechnungen ist zu erwähnen, dass die Nachweise in den geltenden Vorschriften, wie z. B. DIN EN 1993-1-1, auf einer Linearisierung nach Theorie II. Ordnung basieren. Diese Näherung ist daher die Grundlage für die vorschriftengerechte Ermittlung von Verformungen, Schnittgrößen und Verzweigungslasten (Eigenwerten). In der Regel sind Berechnungen nach Theorie II. Ordnung im Hinblick auf baupraktische Anwendungsfälle ausreichend genau, da die Verformungen bei Tragwerken aus Stahl normalerweise relativ klein sind. In seltenen Ausnahmefällen können jedoch auch geometrisch nichtlineare Berechnungen erforderlich sein. Dies ist immer dann der Fall, wenn große oder sogar sehr große Verformungen auftreten. Beispiele dazu sind Kunstwerke, die sich im Wind bewegen und bei denen sich die Einzelteile stark verformen.
Zusammenfassend soll hier Folgendes festgehalten werden:
• Nach wie vor wird die Nachweismethode 1 gemäß Tabelle 1.1am häufigsten verwendet. Für die Systemberechnungen wird dabei linearelastisches Werkstoffverhalten angenommen, auf dieser Grundlage Schnittgrößen und Spannungen ermittelt und dann Spannungsnachweise geführt.
• Vermehrt kommt auch Nachweismethode 2 zum Einsatz, bei der die Tragfähigkeit bis zum Erreichen des ersten Fließgelenkes gesteigert werden kann.
• Bei stabilitätsgefährdeten Stahlkonstruktionen werden das geometrisch nichtlineare Problem linearisiert und die Schnittgrößen nach Theorie II. Ordnung berechnet. Diese Linearisierung wird auch bei der Ermittlung von Verzweigungslasten (Eigenwerten) verwendet.
1.5 Bezeichnungen und Annahmen
Im Folgenden werden Bezeichnungen und Annahmen zusammengestellt, die für Stabtragwerkebenötigt werden. Teilweise gelten sie auch für Flächentragwerke und die FE-Untersuchung von Querschnitten. Zu diesen Themen werden in den Kapiteln 6und 7weitere Bezeichnungen und Annahmen ergänzt. Grundlage für die Bezeichnungen sind DIN 1080 und DIN EN 1993.
Größen im globalen X-Y-Z-Koordinatensystem
Stabtragwerke werden in Stabelemente eingeteilt, die in den Knotenmiteinander verbunden sind. Gemäß Bild 1.2können auch innerhalb der Stabelemente Knoten angeordnet werden (Zwischenknoten). Knoten werden im globalen X-Y-Z-Koordinatensystem (KOS) durch ihre Koordinaten X k, Y kund Z kgemäß Bild 1.4definiert. Darüber hinaus werden auf dieses KOS alle globalen Verformungs- und Lastgrößen in den Knoten bezogen. Aus Gründen der Übersichtlichkeit ist der Index k bei diesen Größen in Bild 1.4weggelassen worden.
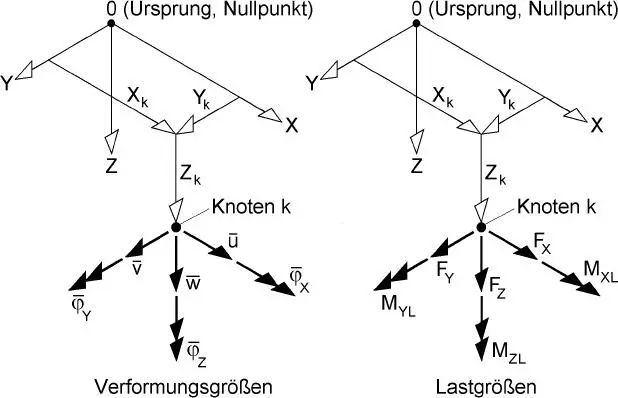
Bild 1.4 Definition von Verformungs- und Lastgrößen im globalen X-Y-Z-Koordinatensystem
Die Verformungsgrößen im globalen KOSwerden durch einen Querstrichgekennzeichnet, der über den Größen steht. Dieser Querstrich wird auch bei Vektoren und Matrizen verwendet, sofern sie für das globale KOS gelten.
Größen in lokalen x-y-z-Koordinatensystemen
Stabelemente werden auf lokale x-y-z-KOS bezogen und als Stabachse die x-Achse durch den Schwerpunkt S definiert. Die Achsen y und z sind die Hauptachsen des Querschnitts. Gemäß Bild 1.5werden einige Verschiebungs- und Schnittgrößen auf den Schwerpunkt S und andere auf den Schubmittelpunkt M (y = y M, z = z M) bezogen. Für die Wölbkrafttorsion wird eine normierte Wölbordinate ω verwendet.
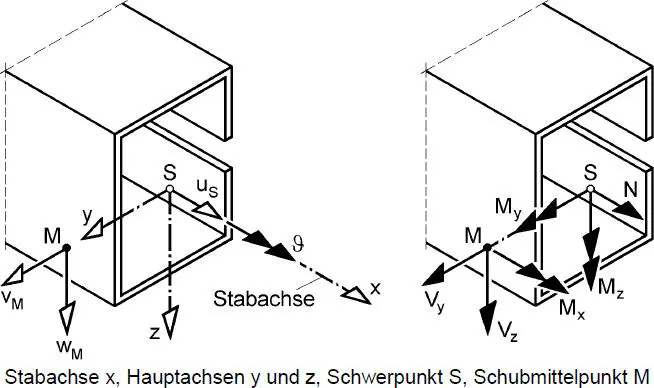
Bild 1.5 Stab im lokalen Koordinatensystem mit Verschiebungs- und Schnittgrößen
Koordinaten, Ordinaten und Bezugspunkte
| x |
Stablängsrichtung im lokalen KOS |
| y, z |
Hauptachsen in der Querschnittsebene (lokales KOS) |
| ω |
normierte Wölbordinate |
| S |
Schwerpunkt |
| M |
Schubmittelpunkt |
Verschiebungsgrößen
| u, v, w |
Verschiebungen in x-, y- und z-Richtung (lokales KOS) |
| φ x= ϑ |
Verdrehung um die x-Achse |
| φ y≅ −w′ |
Verdrehung um die y-Achse |
| φ z≅ −v′ |
Verdrehung um die z-Achse |
| ψ ≅ ϑ′ |
Verdrillung der x-Achse |
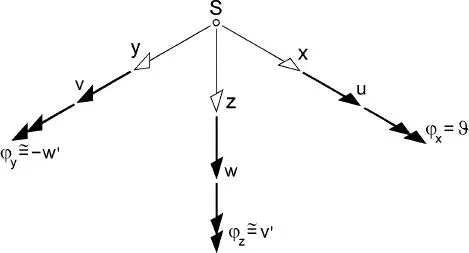
Bild 1.6 Definition positiver Verschiebungsgrößen im lokalen KOS
w′,v′ und ϑ′ sind Ableitungen der Verschiebungsfunktionen nach x, s. Bild 1.6.
Spannungen
| σ x, σ y, σ z |
Normalspannungen |
| τ xy, τ xz, τ yz |
Schubspannungen |
| σ v |
Vergleichsspannung |
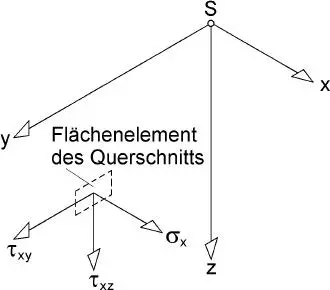
Bild 1.7.Positive Spannungen
Schnittgrößen
Bei der üblichen Definition positiver Schnittgrößen ( Schnittgrößendefinition I ) haben die Schnittgrößen an der negativen SchnittflächeWirkungsrichtungen, die zu den in Bild 1.8festgelegten Richtungen entgegengesetzt sind. Bei der Schnittgrößendefinition IIsind die Wirkungsrichtungen an beiden Schnittflächenwie in Bild 1.8definiert. Die beiden Schnittgrößendefinitionen sind in Bild 1.9für einachsige Biegung mit Normalkraft an einem Stabelement dargestellt. Dabei werden, wie bei der FEM üblich, zur Unterscheidung der Stabelemente und Knoten weitere Indizes verwendet.
| N |
Längskraft, Normalkraft |
| V y, V z |
Querkräfte |
| M y, M z |
Biegemomente |
| M x |
Torsionsmoment DIN EN 1993: T |
| M xp, M xs |
primäres und sekundäres Torsionsmoment DIN EN 1993: Tt, Tw |
| M ω |
Wölbbimoment DIN EN 1993: B |
| M rr |
siehe Tabelle 4.1 |
| Index el: |
Grenzschnittgröße nach der Elastizitätstheorie |
| Index pl: |
Grenzschnittgröße nach der Plastizitätstheorie |
| Index d: |
Bemessungswert ( design) |
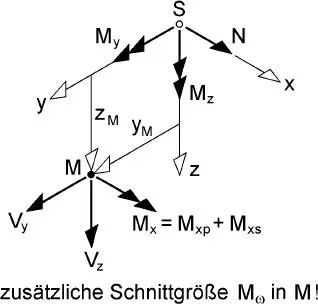
Bild 1.8 Schnittgrößen an der positiven Schnittfläche eines Stabes
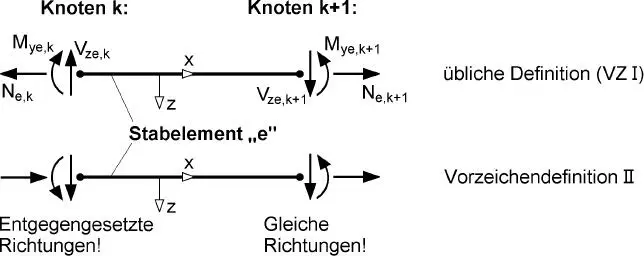
Bild 1.9 Schnittgrößen am Stabelement „e“ für einachsige Biegung mit Normalkraft, Schnittgrößendefinitionen I und II
Lastgrößen
| q x, q y, q z |
Gleichstreckenlasten im lokalen KOS |
| F X, F Y, F Z |
Einzellasten im globalen KOS |
| m x |
Streckentorsionsmoment (konstant) |
| M ωL |
Lastwölbbimoment |
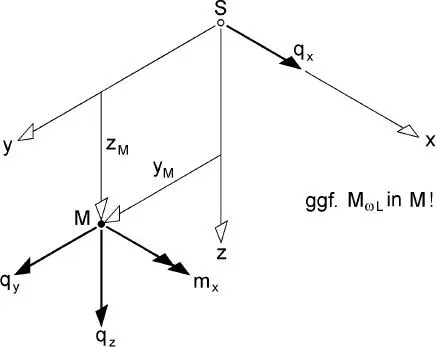
Bild 1.10.Positive Wirkungsrichtungen und Angriffspunkte der lokalen Lastgrößen
Читать дальше



















