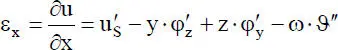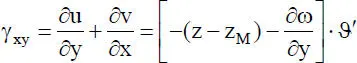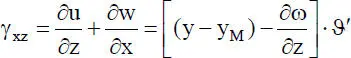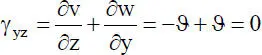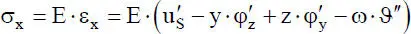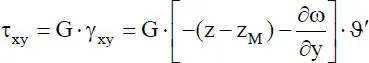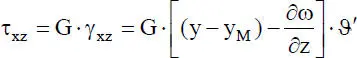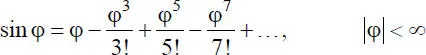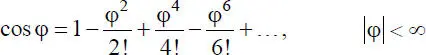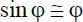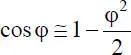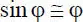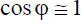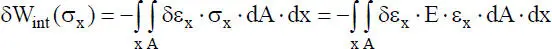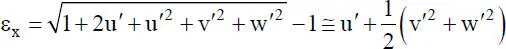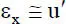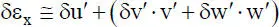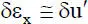Matthias Krauß - Finite-Elemente-Methoden im Stahlbau

(1.4c)

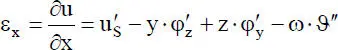
(1.4d)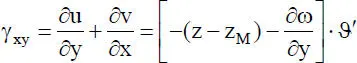

(1.4e)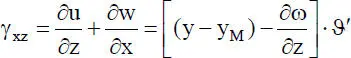

(1.4f)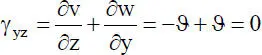

Werkstoffgesetz und Spannungen

Mit dem Werkstoffgesetz wird der Zusammenhang zwischen Spannungen und Verzerrungen beschrieben. Unter Vernachlässigung der Querdehnungen ergeben sich mit dem Hookeschen Gesetz, also dem Materialgesetz für isotropes, linearelastisches Werkstoffverhalten , und den Verzerrungen der Gln. (1.4)folgende Spannungen:

(1.5)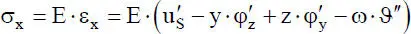

(1.6)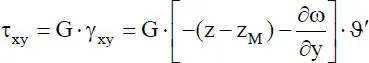

(1.7)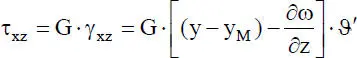

Schnittgrößen

Die Spannungen können zu resultierenden Schnittgrößen zusammengefasst werden. Dabei ist zu beachten, dass die Normalkraft und die Biegemomente im Schwerpunkt angreifen, während die Querkräfte, die Torsionsmomente und das Wölbbimoment im Schubmittelpunkt wirken, vgl. Bild 1.8.

Tabelle 1.4Schnittgrößen als Resultierende der Spannungen

Aufteilung der linearen Theorie schubstarrer Stäbe in vier Teilprobleme

In Tabelle 1.5sind vier Teilprobleme ‒ zweiachsige Biegung mit Normalkraft und Wölbkrafttorsion ‒ der linearen Theorie schubstarrer Stäbe zusammengestellt. Die Tabelle enthält eine Zuordnung der Lastgrößen, Verformungen und Schnittgrößen sowie Angaben zum Gleichgewicht am Stabelement und zur Normalspannung σ x.

Tabelle 1.5 Aufteilung der linearen Stabtheorie nach [12]

Wie im Abschnitt 1.4erläutert, wird das Gleichgewicht bei geometrisch nichtlinearen Berechnungen am verformten System formuliert. Dabei entstehen für die Beschreibung von Verformungen und den damit zusammenhängenden Verzerrungen nichtlineare Beziehungen in Form von trigonometrischen Funktionen. Allgemein lassen sich diese nach [4] durch folgende Reihen entwickeln, was beispielhaft an einer Verdrehung φ veranschaulicht wird:

(1.8)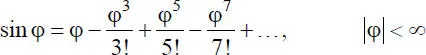

(1.9)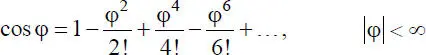

Bei der Theorie II. Ordnung werden die auftretenden geometrischen (trigonometrischen) Beziehungen zur Beschreibung der Verformungen linearisiert, so dass die Theorie damit ein Gleichgewicht am „schwach“ verformten System widerspiegelt, s. Tabelle 1.3. Definitionsgemäß werden als Näherung bei der Formulierung entsprechender Gleichgewichtsbeziehungen höchstens zweifache Produkte der Verformungen berücksichtigt, so dass im Sinne der Linearisierung maximal quadratische Terme einer Verformung auftreten:

(1.10)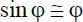

(1.11)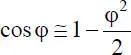

Da von kleinen Verformungen ausgegangen wird, entstehen durch die höheren Reihenglieder Ausdrücke, die im Hinblick auf die Genauigkeit von untergeordneter Bedeutung sind. Bei linearen Formulierungen (vgl. Tabelle 1.3) werden die trigonometrischen Beziehungen stets durch das jeweils 1. Reihenglied beschrieben:

(1.12)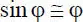

(1.13)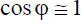

In den Abschnitten 2.4.2und 4.3wird das Gleichgewicht für Stäbe mithilfe des Prinzips der virtuellen Arbeiten formuliert. In den entstehenden Arbeitsgleichungen werden entsprechende Linearisierungen vorgenommen. Um hierzu einen Überblick zu verschaffen, soll am Beispiel der inneren virtuellen Arbeit infolge der Normalspannungen an dieser Stelle vorab die Linearisierung verdeutlicht werden. Gemäß Abschnitt 2.4.2leisten die Normalspannungen an den virtuellen Verzerrungen Arbeit:

(1.14)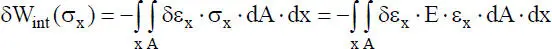

Die Dehnung einer Faser in der verformten Lage kann nach Abschnitt 4.3und den Gln. (4.28) bzw. (4.29) durch folgende kinematische Beziehung beschrieben werden:

(1.15)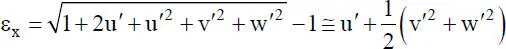

Die in Gl. (1.15)vorgenommene Näherung erfolgt mithilfe einer Reihenentwicklung für die Wurzel und der Berücksichtigung von Reihengliedern, die entsprechend der vorherigen Ausführungen zu maximal zweifachen Produkten der Verformungen führen, vgl. auch Gl. (1.9) mit (1.11). Es handelt sich somit um eine linearisierte kinematische Beziehung. Die lineare Beziehung wird durch den linearen Anteil der Gl. (1.15)beschrieben:

(1.16)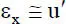

Die virtuellen Verzerrungen δεx ergeben sich aus der 1. Variation der Gln. (1.15)bzw. (1.16). Da für die Variationsrechnung die Regeln der Differentialrechnung gelten, ergibt sich mit der Produktregel:

(1.17)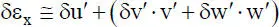

(1.18)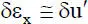

Wie bei den wirklichen Verzerrungen handelt es sich in Gl. (1.17)um die linearisierte und in Gl. (1.18)um die lineare Beschreibung der virtuellen Verzerrungen.

Gemäß Tabelle 1.3werden bei der Theorie I. Ordnung (lineare Theorie) die wirklichen und virtuellen Verzerrungen durch die linearen kinematischen Beziehungen nach Gl. (1.16)bzw. (1.18)beschrieben, was mit Gl. (1.14)zur folgenden inneren virtuellen Arbeit der Normalspannungen führt: