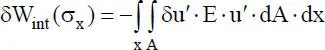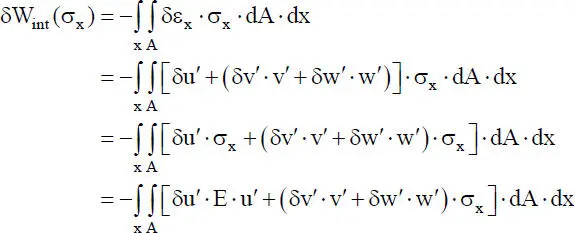(1.19) 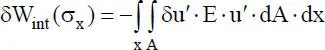
Im Hinblick auf die Theorie II. Ordnung wird nach Tabelle 1.3für die wirklichen Verzerrungen der lineare Zusammenhang nach Gl. (1.16)berücksichtigt, während für die virtuellen Verzerrungen der linearisierte Ausdruck nach Gl. (1.17)genutzt wird. Die innere virtuelle Arbeit nach Gl. (1.19)ergibt sich damit zu:
(1.20) 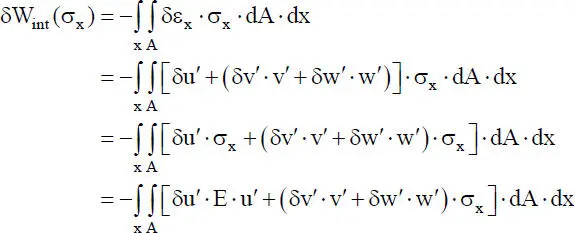
Mit Gl. (1.20)wird deutlich, dass die gewählte Vorgehensweise erneut zu maximal zweifachen Produkten der Verformungen führt. Würden für die wirklichen Verzerrungen ebenfalls linearisierte (und nicht lineare) Ausdrücke berücksichtigt, hätte dies höhere Produkte der Verformungen zur Folge, die im Sinne der Theorie II. Ordnung keine Berücksichtigung fänden. Im Vergleich zu Gl. (1.19)(der Theorie I. Ordnung) sind in Gl. (1.20)zusätzliche Anteile entstanden, die von den Normalspannungen σx abhängen. Da im Zusammenhang mit den wirklichen Spannungen σx die linearen Verzerrungen definiert sind, handelt es sich dabei formal um den Spannungszustand, der der Theorie I. Ordnung entspricht. Im Zusammenhang mit Abschnitt 4.3wird deutlich, dass sich durch Lösen der Flächenintegrale dA in Gl. (1.20)entsprechende Schnittgrößen ergeben, die dann auch nach Theorie I. Ordnung in die entstehende Steifigkeitsbeziehung (geometrische Steifigkeitsmatrix) der Theorie II. Ordnung einfließen.
Für die Berechnungsbeispiele in dem vorliegenden Buch und für ergänzende Untersuchungen wurden im Wesentlichen folgende EDV-Programme angewendet:
• FE-STAB
• FE-Rahmen
• FE-Beulen
• FE-STAB-FZ
• QSW-FE
• QSW-FE ML
Hierbei handelt es sich um Programme, die von wissenschaftlichen Mitarbeitern des Lehrstuhls für Stahl-, Leicht- und Verbundbau der Ruhr-Universität Bochum von 1998 bis 2012 erstellt wurden. Informationen zu FE-STAB, FE-Rahmen, FE-Beulen und vielen weiteren Programmen finden sich auf www.ruhr-uni-bochum.de/stahlbauund www.kindmann.de. Sie stehen dort auch zum kostenlosen Download zur Verfügung. Erläuterungen zum Programm FE-STAB-FZ finden sich in Abschnitt 10.7.2. Für Hinweise zu den Programmen QSW-FE und QSW-FE ML wird auf [37] verwiesen.
Zu Vergleichszwecken und für weiterführende Untersuchungen sind auch Berechnungen mit den folgenden Programmen durchgeführt worden:
| • RSTAB |
Ing.-Software Dlubal GmbH, Tiefenbach |
| • RFEM |
Ing.-Software Dlubal GmbH, Tiefenbach |
| • BT II |
Friedrich + Lochner GmbH, Stuttgart |
| • DRILL |
FIDES DV-Partner GmbH, München |
| • ABAQUS |
ABAQUS, Inc., Providence, Rhode Island, USA |
| • ANSYS |
ANSYS, Inc., Canonsburg, Pennsylvania, USA |
| • SOFiSTiK |
SOFiSTiK AG, Oberschleißheim |
| • LTBeam |
cticm, St Rémy les Chevreuse, Frankreich |
| • EBPlate |
cticm, St Rémy les Chevreuse, Frankreich |
Die Programme LTBeam und EBPlate stehen zum kostenlosen Download zur Verfügung, s. www.cticm.com.
Anmerkung:Das Buch „ Kindmann/Frickel : Elastische und plastische Querschnittstragfähigkeit“ [12] steht unter www.kindmann.dezum kostenlosen Download zur Verfügung.
2
Grundlagen der FEM
2.1 Allgemeines
Wie bereits mit Bild 1.1erläutert, wird ein baustatisches System bei der Berechnung mit der FEMdurch finite Elemente diskretisiert, d. h., das System wird in eine geeignete Anzahl von Elementen unterteilt, die in den Knotenmiteinander verbunden sind und auch Zwischenknoten aufweisen können. Anschließend werden die Schnittgrößen und Verformungen entweder mit dem Weggrößen- oder mit dem Übertragungsverfahren berechnet. Wegen der herausragenden Bedeutung wird im Folgenden ausschließlich das Weggrößenverfahren, das häufig auch Verschiebungsgrößenverfahrengenannt wird, behandelt. Gelegentlich spricht man auch von der Deformationsmethode. Das Übertragungsmatrizenverfahren wird im Hinblick auf einen besonders geeigneten Anwendungsfall in Abschnitt 3.13erläutert.
2.2 Grundideen und Methodik
Wenn man baustatische Systeme mit dem Weggrößenverfahrenuntersucht, so folgt der Berechnungsablauf stets einer gleichbleibenden und sehr schematischen Vorgehensweise. Daraus ergibt sich, in Verbindung mit der universellen Eignung für breit gefächerte Aufgabenstellungen, der überwältigende Erfolg des Verfahrens. Nachteilig ist jedoch neben der relativ stark mathematisch ausgerichteten Lösungsmethode, dass die Grundideen des Verfahrens nicht unmittelbar ersichtlich sind. Da sie für das Verständnis von großer Bedeutung sind, werden sie hier in Zusammenhang mit der Methodik erläutert.
Als Beispiel wird das baustatische System in Bild 2.1abetrachtet. Es handelt sich um einen ebenen Rahmen, für den die Schnittgrößen und Verformungen nach der linearen Stabtheorie ermittelt werden sollen. Der Rahmen hat in den horizontalen und schrägen Teilen unterschiedliche Querschnitte und wird durch die Lastgrößen F und g in der Ebene belastet. Eine wesentliche Grundideeder FEM ist bekanntlich die Aufteilung eines Tragwerks in finite Elemente, die in den Knoten miteinander verbunden sind. Wie Bild 2.1bzeigt, kann der ebene Rahmen in vier Stabelemente mit fünf Knoten aufgeteilt werden. Für baupraktische Berechnungen würde man eine feinere FE-Modellierungvornehmen, weil man dafür Schnittgrößen und Verformungen in engeren Abständen benötigt, die bei der groben Aufteilung in Bild 2.1bmit nachträglichen Berechnungen ermittelt werden müssen.
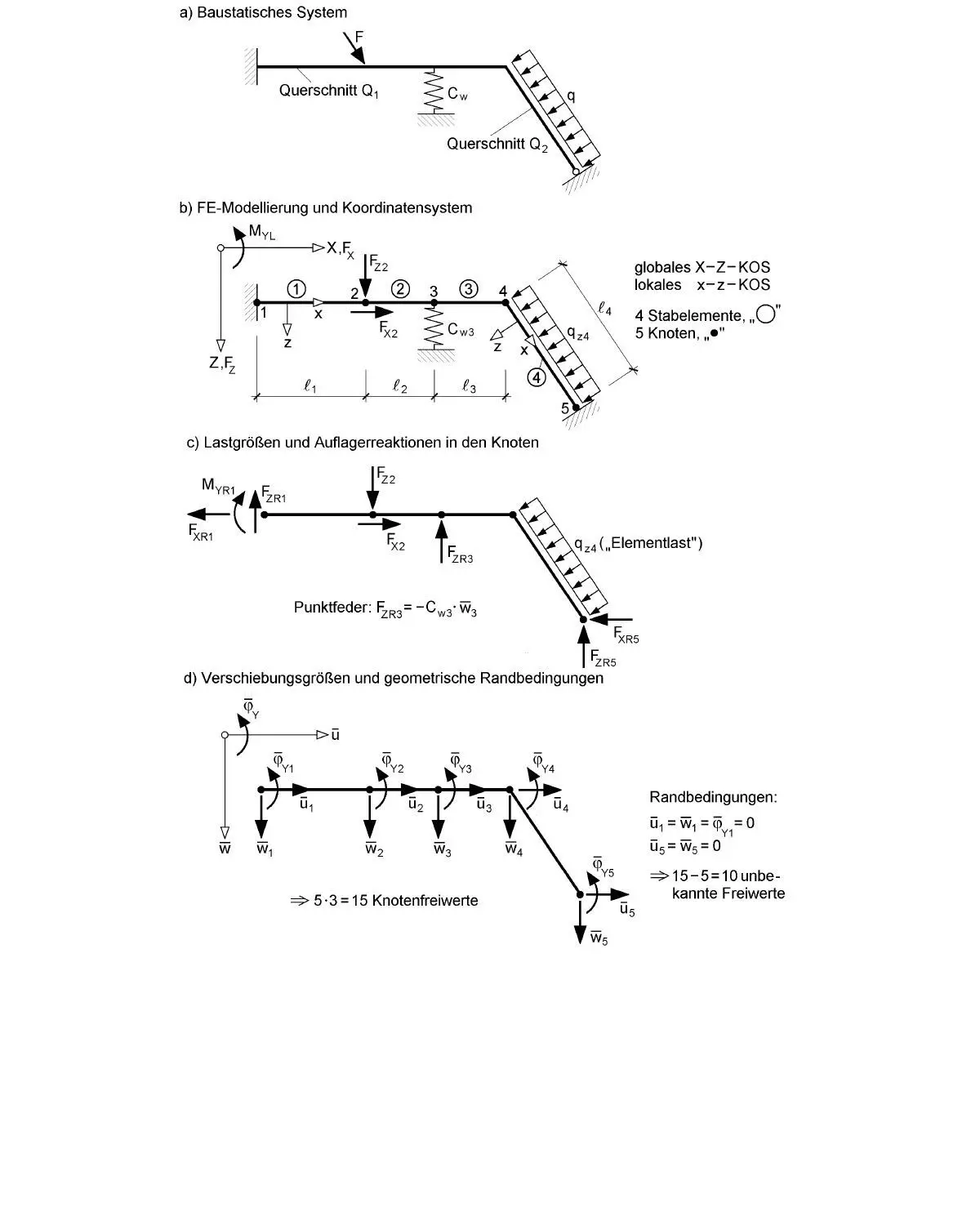
Bild 2.1 Grundlegendes Beispiel zum Verständnis der FEM
Erforderlich bzw. zweckmäßig ist es, Knotenwie folgt anzuordnen:
bei Lagern, Einzellasten und Punktfedern
am Anfang und Ende von Streckenlasten, Streckenfedern und Schubfeldern
bei Querschnittssprüngen
bei Richtungsänderungen der Stäbe (Knicke, Ecken)
Der Vollständigkeit halber sei erwähnt, dass man bei den Lasten auf die Knoten durchaus verzichten kann, wenn man wie in Abschnitt 3.9erläutert die entsprechenden Umrechnungen vornimmt. Knoten 2 in Bild 2.1bist daher nicht zwingend erforderlich.
Lagerbedingungen sind im Sinne der FEM geometrische Randbedingungen. Sie beziehen sich wie auch Einzellastgrößen und Punktfedern stets auf das globale Koordinatensystemund haben daher zu X und Z entsprechende Richtungen. Aus diesem Grund ist die Einzellast F in Bild 2.1ain ihre Komponenten F X2und F Z2zerlegt worden ( Bild 2.1c), und die Vorzeichen sind positiv, wenn die Wirkungsrichtungen mit X und Z übereinstimmen. Auflagerreaktionen (mit dem Index „R“ gekennzeichnet), sind entgegen X und Z positiv definiert.
Im Zusammenhang mit den Stabelementen werden lokale x-z-Koordinatensystemeverwendet und sowohl Streckenlasten als auch Streckenfedern den Stabelementen zugeordnet. Die „ Elementlast“ q z4in Bild 2.1cbezieht sich daher auf die lokale z-Ordi-nate von Element 4. Sie wird später (s. Bild 2.3bis Bild 2.5) in äquivalente Knotenlasten umgerechnet, die sich auf das globale X-Z-KOS beziehen. Die Auflagerreaktionen in Bild 2.1csind unbekannte Größen, die bekanntlich mit den Lastgrößen im Gleichgewicht stehen müssen.
Читать дальше