Bei Eigenwertproblemenist prinzipiell ebenfalls die beschriebene Vorgehensweise wie für Berechnungen nach Theorie II. Ordnung durchzuführen. Im 2. Durchlauf entfällt jedoch der Lastvektor gemäß Pkt. 5, und es wird mit 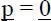 das Eigenwertproblem
das Eigenwertproblem
(2.7) 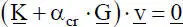
formuliert. Gl. 2.7bildet den Ausgangspunkt für die Ermittlung des „ Verzweigungslastfaktors “ α cr(Eigenwert) und der Eigenform  . In der Regel werden der kleinste positive Eigenwert und die zugehörige Eigenform gesucht. Die Lösung von Eigenwertproblemen wird im Kapitel 9behandelt, s. auch Abschnitte 4.9und 4.10.
. In der Regel werden der kleinste positive Eigenwert und die zugehörige Eigenform gesucht. Die Lösung von Eigenwertproblemen wird im Kapitel 9behandelt, s. auch Abschnitte 4.9und 4.10.
2.4 Gleichgewicht
2.4.1 Vorbemerkungen
Wenn Tragwerke belastet werden, treten aufgrund der einwirkenden Lastgrößen Verformungen auf. Als Reaktion entstehen im Tragwerk Spannungen und Dehnungen, die zu den Schnitt- und Verformungsgrößen korrespondieren, und das Tragwerk befindet sich im Gleichgewicht. Die Formulierung der Gleichgewichtsbedingungen ist in der FEM eine zentrale Aufgabe und man benötigt daher entsprechende Prinzipien und Methoden. Üblich sind:
Prinzip der virtuellen Arbeit
Prinzip vom Minimum der potentiellen Energie
Gleichgewicht am differentiellen Element/Differentialgleichungen
Die Differentialgleichungen (DGLn) werden in Abschnitt 2.7 dazu herangezogen, möglichst zutreffende Ansatzfunktionen für die Verformungsgrößen zu identifizieren. Dazu sind sie gut geeignet, weil analytische Lösungen der DGLn für einige wichtige Sonderfälle bekannt sind. Für andere Fälle, wie z. B. die zweiachsige Biegung mit Normalkraft und Torsion nach Theorie II. Ordnung bei Stäben, liegen keine Lösungen vor und es ist daher zweckmäßig, allgemeine Gleichgewichtsprinzipien zu verwenden. Im vorliegenden Buch wird zur Formulierung der Gleichgewichtsbedingungen durchgängig die virtuelle Arbeit verwendet.
2.4.2 Prinzip der virtuellen Arbeit
Zunächst soll der Begriff „virtuelle Arbeit“ verdeutlicht werden. Bild 2.6zeigt in diesem Zusammenhang die Unterschiede zwischen der Eigenarbeit, der Verschiebungsarbeit und der virtuellen Arbeit. Bei Tragwerken mit linearelastischem Verhalten steht die Tragwerksverformung im proportionalen Verhältnis zur aufgebrachten Last. Wird entsprechend Bild 2.6aeine Kraft F auf einen Träger aufgebracht und stetig gesteigert, so ergibt sich das angedeutete Last-Verformungs-Diagramm und als geleistete Arbeit die sogenannte Eigenarbeitmit 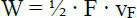 .
.
Der Träger wird nun durch weitere Kräfte belastet (s. Bild 2.6b), die auch an der Stelle, an der die Kraft F wirkt, eine Verformung hervorrufen. Mit der dabei auftretenden zusätzlichen Verformung vF erhält man wegen F = konst. die VerschiebungsarbeitW = F ∙ v F, die dem bekannten Zusammenhang „Arbeit = Kraft mal Weg“ entspricht.
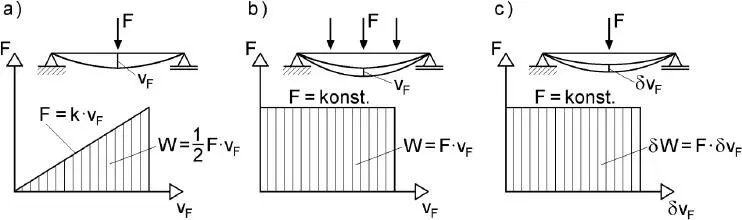
Bild 2.6 a) Eigenarbeit W b) Verschiebungsarbeit W c) virtuelle Arbeit δW
Wie in Bild 2.6cskizziert führt das Aufbringen einer gedanklichen/gedachten Verformung δvF auf entsprechende Weise zu einer virtuellen ArbeitδW = F ∙ δv F. Zur Verdeutlichung wird dieser Zusammenhang erneut in Bild 2.7aufgegriffen, in dem die Kraft F inRichtung ihrer Wirkungslinie verschoben und der Verschiebungsweg mit δu Fbezeichnet werden. Die gedanklich vorgenommene Verschiebung δu Fführt dann zur virtuellen Arbeit δW = F ∙ δu F.

Bild 2.7 Virtuelle Arbeit einer Kraft
In vergleichbarer Weise kann auch die virtuelle Arbeit ermittelt werden, die eine Normalkraft bei der virtuellen Verschiebung eines Querschnitts leistet. Da N vereinbarungsgemäß im Schwerpunkt S angreift, wird die virtuelle Verschiebung in Bild 2.8mit δu Sbezeichnet. Rechts daneben wird die Normalspannung infolge N beispielhaft für die Ermittlung der inneren virtuellen Arbeit betrachtet. Sie ist als Reaktion auf die einwirkenden Kräfte negativ und das Produkt σ x∙ δε xüber den gesamten Stab zu integrieren . So wie Verschiebungswege zu Kräften korrespondieren, gehören bei der inneren virtuellen Arbeit Dehnungen zu Spannungen.
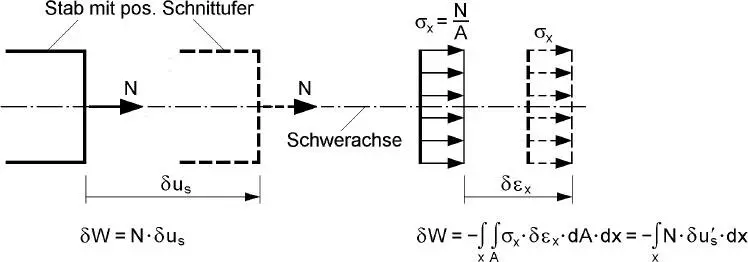
Bild 2.8 Virtuelle Arbeit infolge Normalkraft N und Spannung σ x
Ausgangspunkt des Prinzips der virtuellen Arbeit ist ein statisches System, das sich im Gleichgewichtszustand befindet, d. h. „reale“ äußere angreifende Lasten stehen im Gleichgewicht mit „realen“ Schnittgrößen bzw. entsprechenden Spannungen. Bild 2.9zeigt dies am Beispiel eines Einfeldträgers mit Gleichstreckenlast. Das in Teilbild a) dargestellte System verformt sich durch die Last entsprechend Teilbild b) und die Verformungen w sind mit einem Dehnungs- bzw. Spannungszustand verbunden – das Tragwerk befindet sich im Gleichgewicht.
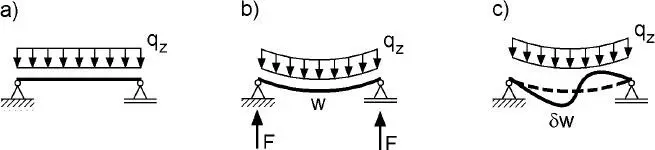
Bild 2.9 Zum Prinzip der virtuellen Arbeit
Das im Gleichgewicht befindliche System wird nun gedanklich (virtuell) einem beliebigen Verformungs- und damit verbundenen Verzerrungszustand unterworfen, der die Rand- bzw. Lagerungsbedingungen des statischen Systems erfüllt. Für das Beispiel des Einfeldträgers wird dies in Bild 2.9cdurch eine virtuelle Verformung δw veranschaulicht. Durch die gedankliche Auslenkung des Systems leisten die „realen“ äußeren Lasten Arbeit an den virtuellen Verformungen, was als „äußere virtuelle Arbeit“ bezeichnet wird. Gleiches gilt für die „realen“ Spannungen, die an den virtuellen Verzerrungen sogenannte „innere virtuelle Arbeit“ leisten. Das Prinzip der virtuellen Arbeit besagt, dass, sofern sich der Körper im Gleichgewichtszustand befindet (entsprechend Bild 2.9b), der Betrag beider Arbeitsanteile gleich groß sein muss. Da die innere virtuelle Arbeit als Reaktion auf die einwirkenden Kräfte negativ definiert ist, befindet sich ein Tragwerk somit im Gleichgewicht, wenn die Summe der virtuellen Arbeiten gleich null ist. Die Bedingung
(2.8) 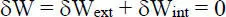
ist daher die allgemeine Forderung, dass Gleichgewicht vorhanden ist. In Gl. (2.8)ist δW extdie virtuelle Arbeit der äußeren eingeprägten Kräfte  und δW intdie virtuelle Arbeit aufgrund der Spannungen
und δW intdie virtuelle Arbeit aufgrund der Spannungen 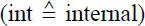 .
.
Читать дальше

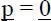 das Eigenwertproblem
das Eigenwertproblem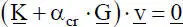
 . In der Regel werden der kleinste positive Eigenwert und die zugehörige Eigenform gesucht. Die Lösung von Eigenwertproblemen wird im Kapitel 9behandelt, s. auch Abschnitte 4.9und 4.10.
. In der Regel werden der kleinste positive Eigenwert und die zugehörige Eigenform gesucht. Die Lösung von Eigenwertproblemen wird im Kapitel 9behandelt, s. auch Abschnitte 4.9und 4.10.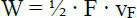 .
.



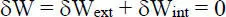
 und δW intdie virtuelle Arbeit aufgrund der Spannungen
und δW intdie virtuelle Arbeit aufgrund der Spannungen  .
.










