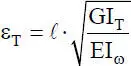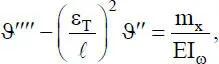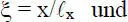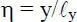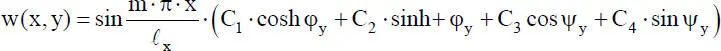Matthias Krauß - Finite-Elemente-Methoden im Stahlbau

Wenn man nun eine Stabkennzahl

(2.52)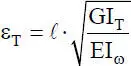

für Torsion definiert, ergibt sich die DGL

(2.53)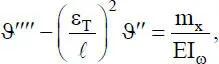

die mit der DGL (2.41)formal übereinstimmt. Ihre Lösung führt daher zu einer Funktion ϑ(ξ), die wie bei der „Biegung mit Zugnormalkraft nach Theorie II. Ordnung“ die Hyperbelfunktionen sinh(ε T⋅ ξ) und cosh(ε T⋅ ξ) enthält und im Übrigen formal mit Gl. (2.42)übereinstimmt. Die Herleitung der Elementsteifigkeitsmatrix für die Wölbkrafttorsion erfolgt in Abschnitt 3.2.4.

Biegedrillknicken und andere kombinierte Beanspruchungen

Bis auf die zuvor betrachteten Sonderfälle liegen keine weiteren Lösungen für andere Problemstellungen vor. Dennoch kann davon ausgegangen werden, dass beim Biegedrillknicken und auch bei kombinierten Beanspruchungen, die Untersuchungen zur Stabilität oder nach Theorie II. Ordnung erfordern, ebenfalls trigonometrische und Hyperbelfunktionen für die Beschreibung der Verformungen benötigt werden. Da bei diesen Problemstellungen jedoch nur die Polynomansätze verwendet werden können, ist auf eine ausreichend feine FE-Modellierung zu achten. Als Orientierungshilfe können die drei Sonderfälle herangezogen werden. Im Zweifelsfall ist eine feinere Modellierung zu wählen oder schrittweise zu verfeinern, s. dazu auch Abschnitt 5.2.6.

Für baustatische Untersuchungen von Plattenwerden i. d. R. dreieckige oder vier-eckige Plattenelemente mit geraden Kanten verwendet, weil gekrümmte Kanten bei baupraktischen Aufgabenstellungen kaum vorkommen. Bild 2.14zeigt ausgewählte Dreieck- und Rechteckelemente, die sich bezüglich der Anzahl der Knoten und Anzahl der Freiwerte (Verformungsgrößen) unterscheiden.

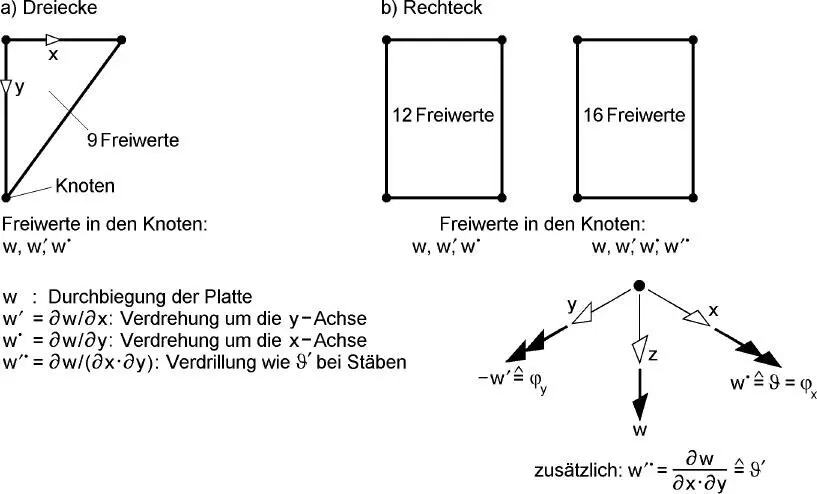
Bild 2.14 Dreieck- und Rechteckelemente für Platten

Die Platten werden hier in der x-y-Ebene betrachtet und bei den Plattenelementen die dimensionslosen Koordinaten

(2.54)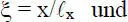

(2.55)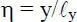

verwendet. Mit diesen Bezeichnungen ergeben sich die in Bild 2.15dargestellten Kombinationen von ξ n⋅ η mfür Flächenelemente, wenn Polynomfunktionen zur Be-schreibung der Verformungen eingesetzt werden. Als Ergänzung dazu zeigt Bild 2.16zwei-, drei- und viergliedrige Ansätze in beiden Richtungen für w(ξ, η) und die Poly-nomterme, die dabei auftreten. Wenn man diese Terme vollständig erfassen will, sind entsprechende Elemente mit Knoten und Freiwerten zu wählen. Dies ist für die zutreffende Beschreibung der Durchbiegungen von großer Bedeutung. Sinnvoll sind daher unter diesem Aspekt Flächenelemente mit 4, 9 oder 16 Freiwerten , s. auch Bild 2.16.

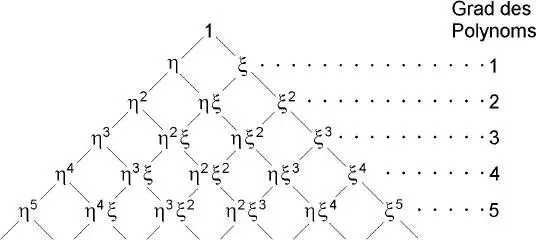
Bild 2.15 Polynomterme für Polynomfunktionen bei Flächenelementen (Pascalsches Polynomschema)

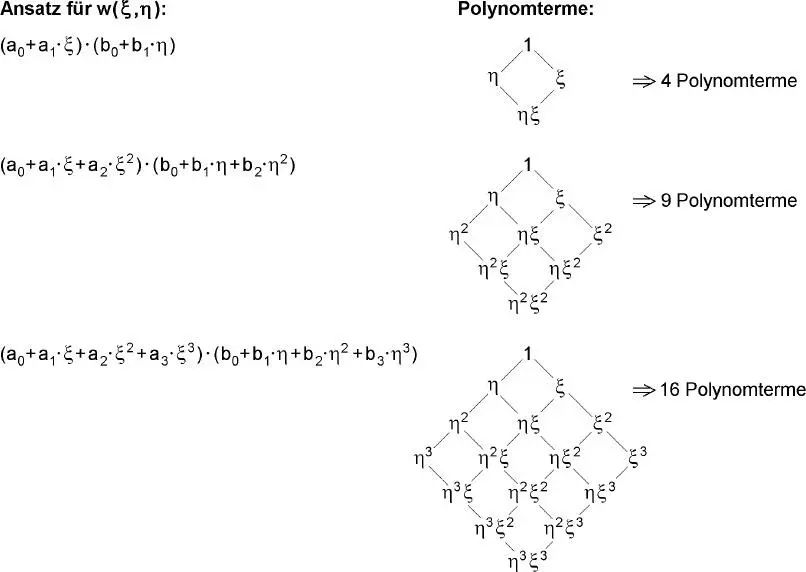
Bild 2.16 Ansätze für w(ξ, η) und auftretende Polynomterme

Die Plattenbiegungentspricht dem Tragverhalten von Biegeträgern, wenn man zusätzlich den Lastabtrag in y-Richtung berücksichtigt. Als Beispiel seien Trägerroste genannt, die unter Verwendung von Biegeträgern in x- und y-Richtung für längs- und querausgesteifte Platten eingesetzt werden. Es kann daher auf die Herleitungen für die Biegung von Stäben in Abschnitt 2.5.2zurückgegriffen werden. Gl. (2.29)zeigt, dass das viergliedrige Polynom die Lösung des Problems genau erfasst und daher der Ansatz für w(ξ, η) in Bild 2.16unten für die Plattenbiegung zu den Biegeträgern korrespondiert. Aufgrund der jeweils viergliedrigen Ansätze treten bei der Produktbildung 16 Polynomterme auf, so dass ein finites Plattenelement möglichst 16 Freiwerte aufweisen sollte. Diese Forderung wird durch das Rechteckelement mit vier Knoten und jeweils vier Freiwerten in Bild 2.14rechts am besten erfüllt. Ein weiterer Vorteil ist, dass dieses Plattenelement unmittelbar mit einem Stabelement für einachsige Biegung mit Wölbkrafttorsion kombiniert werden kann, was für ausgesteifte Platten von großer Bedeutung ist.

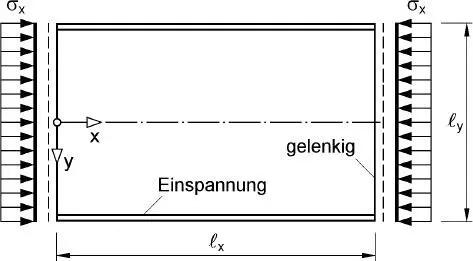
Bild 2.17 Beulfeld mit eingespannten Längsrändern

Wie schon bei der Plattenbiegung kann auch das Plattenbeulenmit den entsprechenden Problemstellungen bei Stäben verglichen werden. Dazu werden hier die homogene DGL (2.18)für das Plattenbeulen und die DGLn (2.15)und (2.16)für das Biegeknicken von Stäben bzw. die Biegung mit Druck- oder Zugkraft nach Theorie II. Ordnung herangezogen. Der Vergleich zeigt, dass das Plattenbeulen für τ xy= 0 und Druckspannungen σ xund σ ywie ein „zweidimensionales Biegeknicken“ aufgefasst werden kann. Mit Abschnitt 2.5.3folgt daraus, dass die Verformungsfunktion w(ξ, η) beim Plattenbeulen wie beim Biegeknicken von Stäben die trigonometrischen Funktionen sin und cos enthält. Darüber hinaus können auch die Hyperbelfunktionen sinh und cosh zur Beschreibung der „Beulverformungen“ (Eigenformen) notwendig sein, weil bereichsweise Zugspannungen auftreten können. In diesem Zusammenhang ist auch ein von Petersen [51] untersuchtes Beispiel interessant. Er löst das Beulproblem für das Einzelfeld in Bild 2.17mit eingespannten Längsrändernund weist nach, dass der Produktansatz

(2.56)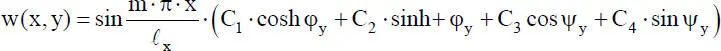

eine zutreffende Lösung ist. Wie man sieht treten die Funktionen sin, cos, sinh und cosh auf.

Da ein finites Element für das Plattenbeulen universell einsetzbar sein muss, empfiehlt sich der Ansatz mit Polynomfunktionen in ξ- und η-Richtunggemäß Bild 2.16unten. Durch eine entsprechend feine Elementierung können die oben erwähnten Verläufe der Funktionen sin, cos, sinh und cosh näherungsweise, aber mit ausreichender Genauigkeit erfasst werden. Grundsätzlich gilt, dass die Aufteilung in finite Elemente fein genug sein muss, um die auftretende Beulfigur in zutreffender Weise beschreiben zu können. Als Orientierungshilfe für die Wahl der Elementlängen a und b kann man auch auf die Bedingungen ε D≤ 1,0 und ε Z≤ 1,0 in Abschnitt 2.5.3für Stabelemente zurückgreifen. Bei analoger Vorgehensweise erhält man folgende Bedingung für die Elementlänge ℓ x: