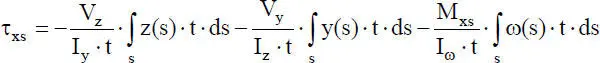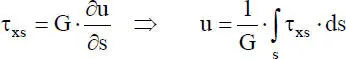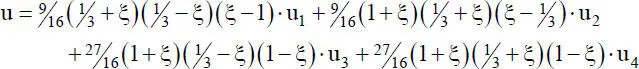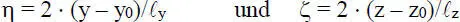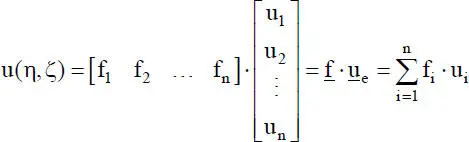Matthias Krauß - Finite-Elemente-Methoden im Stahlbau

St. Venantsche Torsion

Gemäß Abschnitt 7.4setzen sich die Schubspannungen der St. Venantschen (primären) Torsion bei dünnwandigen Querschnitten aus zwei Anteilen zusammen. In den rechteckigen Teilquerschnitten (offene Querschnitte) ergeben sich Schubspannungen, die auf der Mittellinie der Bleche in weiten Bereichen gleich null sind. Aufgrund der Reduzierung des Querschnitts auf seine Mittellinie können sie durch entsprechende finite Elemente mit den Freiwerten u nicht erfasst werden. Sie müssen deshalb mit anderen Methoden ermittelt werden. In den Hohlzellen von dünnwandigen Querschnitten sind die Schubspannungen infolge St. Venantscher Torsion über die Blechdicke und in Blechlängsrichtung konstant. Wegen τ xs= G ⋅ γ xsund γ xs= ∂u/∂s + ∂v/∂x ergeben sich nach der Integration linear veränderliche Verschiebungen u, so dass wie bei der Wölbordinate ω ein Querschnittselement nach Tabelle 2.4links bzw. Gl. (2.63)ausreicht. Die Thematik wird in Abschnitt 7.3vertieft.

Querkräfte und sekundäre Torsion

Zur Berechnung von Schubspannungen, die sich infolge von Querkräften und der sekundären Torsion ergeben, werden in Abschnitt 7.3die zugehörigen Schubverformungen herangezogen. Es ist allgemein üblich, diese Schubspannungen in dünnwandigen Querschnitten durch Gleichgewichtsbetrachtungen zu bestimmen, was nach [12] zu der folgenden Bestimmungsgleichung führt:

(2.64)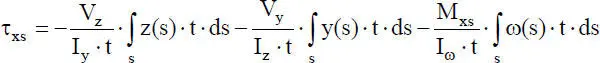

Für geradlinige Querschnittsteile mit gleichbleibender Blechdicke t sind die Faktoren vor den Integralen konstante Größen. Daraus ergibt sich, dass der Verlauf der Schubspannungen nur von den Integralen abhängt. Da die Ordinaten z(s), y(s) und ω(s) einen konstanten oder linear veränderlichen Verlauf haben, ergibt sich für die Schubspannungen τ xsein linear veränderlicher oder quadratischer Verlauf. Mit der Definition der Schubspannungen in Abhängigkeit von den Schubverformungen nach Gl. (7.21) in Abschnitt 7.4.1 folgt

(2.65)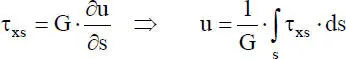

und daher ein quadratischer oder kubischer Verlauf der Verschiebungen u(s). Somit gelingt eine genaue Beschreibung mit dem Verschiebungsansatz in Tabelle 2.4rechts:

(2.66)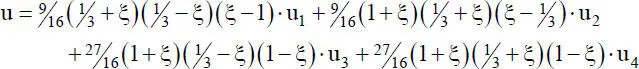

Der Verlauf der in Gl. (2.66)enthaltenen Formfunktionen ist beispielhaft für f 1und f 3in Bild 2.20bdargestellt.

Im Abschnitt 2.5.5sind Ansätze für die Verschiebungen u(x, s) zur Untersuchung von dünnwandigen Stabquerschnitten formuliert worden. Im Vergleich zu den dünnwandigen Querschnitten ist es bei den dickwandigen nicht ausreichend, nur die Profilmittellinie zu betrachten. Daher sind bei diesen Querschnitten zur Beschreibung der Verschiebungen u zweidimensionale Interpolationspolynome erforderlich, mit denen auch der Funktionsverlauf über die Dicke erfasst werden kann.

Betrachtet man zunächst ein zweidimensionales rechteckiges Element, dessen Ränder mit dem y-z-Hauptachsensystem eines Querschnitts zusammenfallen, so können die Ordinaten des Hauptsystems durch die dimensionslosen Elementordinaten

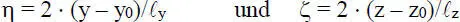
ersetzt werden. Bild 2.21zeigt drei rechteckige Elemente mit 4, 9 und 16 Freiwerten für die Verschiebung u.

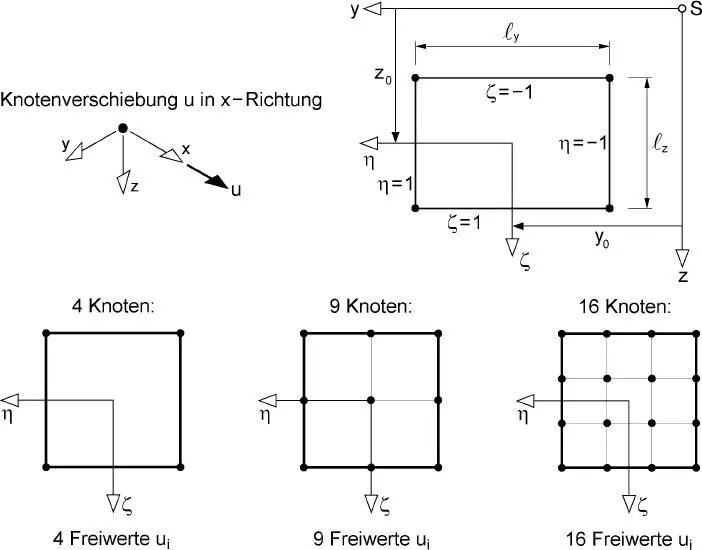
Bild 2.21 Zweidimensionale Elemente für Querschnitte und Freiwerte u

Bei den dünnwandigen Querschnitten konnte direkt für die unterschiedlichen Pro-blemstellungen, d. h. für die Wölbordinate ω sowie die Schubverformungen u infolge primärer Torsion, Querkraft und sekundärer Torsion, angegeben werden, mit welchen Polynomen die Verschiebungen u(x, s) genaubeschrieben werden können. Da der Verlauf der Verschiebungen u(x, y, z) von der Geometrie eines Querschnitts abhängt, ist dies für dickwandige Querschnitte nicht möglich. Er kann nur für grundlegende Formen (z. B. für Rechtecke oder gleichseitige Dreiecke) analytisch angegeben wer-den. Aus diesem Grund kann a priori nicht festgelegt und verallgemeinert werden, welcher Polynomgrad sich für die Ansatzfunktionen am besten eignet. Mit einem gewählten Verschiebungsansatz kann daher im Allgemeinen nur eine Näherungslösung erzielt werden, die bei einer Verfeinerung der FE-Modellierung jedoch zur genauen Lösung konvergieren soll.

Damit dies gewährleistet ist, muss der Verschiebungsansatz Anforderungen bzgl. der Stetigkeit erfüllen. Betrachtet man die Grundgleichungen der beliebigen dickwandigen Querschnitte (s. Abschnitt 7.5.2), so wird deutlich, dass in der virtuellen Arbeit die Verschiebungen u und die ersten Ableitungen der Verschiebung auftreten. Für den Verschiebungsansatz bedeutet dies, dass er in den Funktionswerten stetig verlaufen muss, damit die ersten Ableitungen und daher auch die Verzerrungen stets endliche Werte ergeben. Sie dürfen natürlich nicht unendliche Werte annehmen, da das einer Klaffung im Inneren des Elements entsprechen würde. Man spricht hierbei von einer C0-Stetigkeit . Gleichzeitig muss der Verschiebungsansatz auch mindestens einmal differenzierbar sein, ohne zu null zu werden. Beides wird durch die Verwendung der Lagrangeschen Interpolationspolynomen sichergestellt, die im Zusammenhang mit den dünnwandigen Querschnitten bereits für eindimensionale Problemstellungen in Abschnitt 2.5.5behandelt worden sind.

Tabelle 2.5 Lagrangesche Interpolationspolynome für Flächenelemente

Für die hier benötigten zweidimensionalen Elemente sind die Formfunktionen f ides bilinear veränderlichen und biquadratischen Ansatzes in Tabelle 2.5zusammengestellt und in den Bildern 2.22und 2.23die Verläufe beispielhaft grafisch dargestellt. Die Formulierung der Funktionen erfolgt unter der Verwendung der dimensionslosen Koordinaten η und ζ, deren Ursprung in der Mitte der entsprechenden Intervalle ‒1 ≤ η ≤ 1 und ‒1 ≤ ζ ≤ 1 liegt. Damit ergibt sich der Funktionsverlauf zur Beschreibung der Verschiebungen u für ein Element mit n Knoten:

(2.67)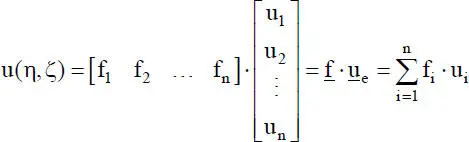

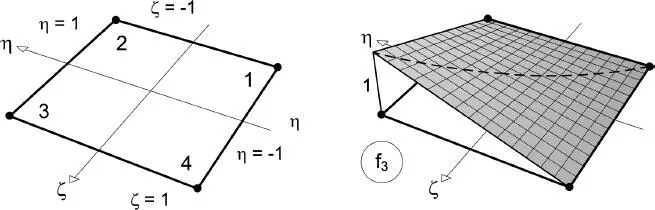
Bild 2.22 Formfunktion f 3beim bilinear veränderlichen Funktionsverlauf

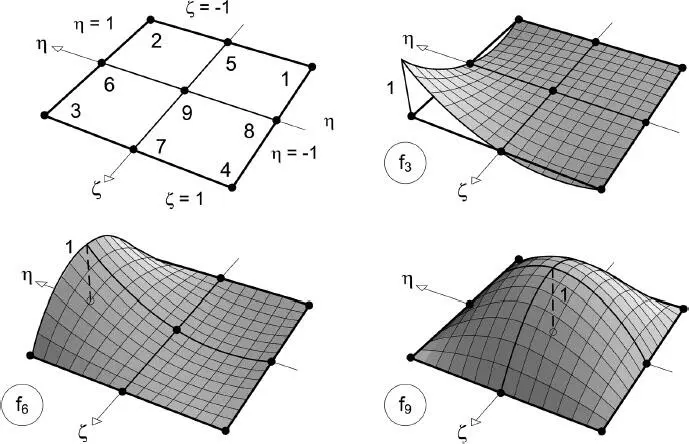
Bild 2.23 Formfunktionen f 3, f 6und f 9beim biquadratischen Funktionsverlauf