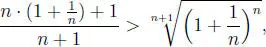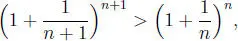Ahora tomemos los n números reales positivos:
a , a 3, a 4, ··· , an , an + 1,
Si todos ellos fueran iguales a 1 tendríamos:
a + a 3+ a 4+ ··· + an + an + 1= n,
pero, por (1.10):
a = a 1· a 2< a 1+ a 2− 1,
luego:
n = a + a 3+ a 4+ ··· + an + an + 1< a 1+ a 2− 1 + ··· + an + an + 1,
y, por lo tanto, resulta:
a 1+ a 2+ ··· + an + an + 1> n + 1 .
Si este no es el caso, entonces no todos son iguales a 1 y por hipótesis inductiva se tendría que:
a + a 3+ a 4+ ··· + an + an + 1> n ,
y, al usar nuevamente (1.10), se llega a que:
a 1+ a 2+ ··· + an + an + 1> n + 1.
Con lo que el problema queda resuelto.
Definición 1.3.1(1) Sean a 1, a 2, ··· , an ∈ 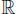 se define el medio aritmético entre ellos como:
se define el medio aritmético entre ellos como:
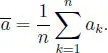
(2) Sean a 1, a 2, ··· , an ∈ 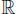 + se define el medio geométrico entre ellos como:
+ se define el medio geométrico entre ellos como:
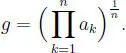
(3) Sean a 1, a 2, ··· , an ∈ 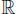 − {0} se define el medio armónico entre ellos como:
− {0} se define el medio armónico entre ellos como:
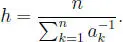
Problema 1.3.19 Sean a 1, a 2, · ·· , an ∈ 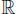 +, entonces:
+, entonces:
Solución:
Si a 1, a 2, ··· , an ∈ 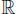 +son todos iguales la respuesta es evidente, pues los medios serán iguales. Entonces nos pondremos en el caso en que no todos son iguales entre sí.
+son todos iguales la respuesta es evidente, pues los medios serán iguales. Entonces nos pondremos en el caso en que no todos son iguales entre sí.
Sea bk = 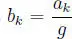 para k = 1, 2, 3, ··· , n . Como g y ak son positivos resulta bk positivo, además no todos son iguales entre sí porque los ak no lo son, luego, en particular, no pueden ser todos iguales a 1. Por otro lado:
para k = 1, 2, 3, ··· , n . Como g y ak son positivos resulta bk positivo, además no todos son iguales entre sí porque los ak no lo son, luego, en particular, no pueden ser todos iguales a 1. Por otro lado:
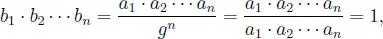
en conclusión, por el anterior problema resuelto, se obtiene:
b 1+ b 2+ ··· + bn > n,
y por lo tanto, llegamos a:
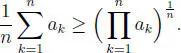
Para la segunda parte, consideremos los números ck = 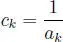 tomando k los valores k = 1, 2, 3, ··· , n . Otra vez resulta que todos los ck son positivos y si son todos iguales, el resultado es claro. Supondremos, entonces que no todos son iguales entre sí. A causa del resultado anterior, se obtiene:
tomando k los valores k = 1, 2, 3, ··· , n . Otra vez resulta que todos los ck son positivos y si son todos iguales, el resultado es claro. Supondremos, entonces que no todos son iguales entre sí. A causa del resultado anterior, se obtiene:
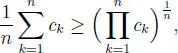
o sea:
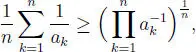
con lo que:
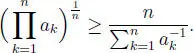
Problema 1.3.20 Demostrar que:
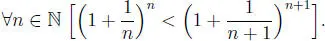
Solución:
Considerando la desigualdad medio aritmético medio geométrico, demostrada en el anterior problema resuelto, tenemos que:
Siendo x 1, x 2, ··· , xn , x n + 1∈  +(no todos iguales), entonces:
+(no todos iguales), entonces:
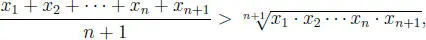
en ella hacemos: x 1= x 2= ··· = xn = 1 + n 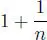 , xn + 1= 1 se obtiene:
, xn + 1= 1 se obtiene:
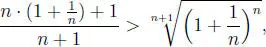
o sea:
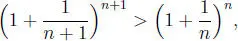
lo que se deseaba.
Problema 1.3.21 Sean a, b ∈  +, n ∈ Nentonces:
+, n ∈ Nentonces:
a < b ←→ an < bn.
Solución:
Parte (1)
Supongamos que a < b ; demostraremos por inducción que an < bn .
Si n = 1 se tiene que an = a < b = bn .
Supongamos ahora que an < bn , demostraremos que an + 1< b n + 1.
Pues bien, se tiene:
a n + 1= an · a < bn · a < bn · b = b n + 1.
Por lo tanto, para todo par de reales positivos a, b y para todo natural n se cumple que:
Читать дальше

 se define el medio aritmético entre ellos como:
se define el medio aritmético entre ellos como: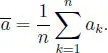
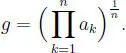
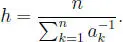
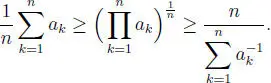
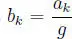 para k = 1, 2, 3, ··· , n . Como g y ak son positivos resulta bk positivo, además no todos son iguales entre sí porque los ak no lo son, luego, en particular, no pueden ser todos iguales a 1. Por otro lado:
para k = 1, 2, 3, ··· , n . Como g y ak son positivos resulta bk positivo, además no todos son iguales entre sí porque los ak no lo son, luego, en particular, no pueden ser todos iguales a 1. Por otro lado: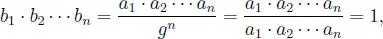
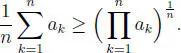
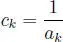 tomando k los valores k = 1, 2, 3, ··· , n . Otra vez resulta que todos los ck son positivos y si son todos iguales, el resultado es claro. Supondremos, entonces que no todos son iguales entre sí. A causa del resultado anterior, se obtiene:
tomando k los valores k = 1, 2, 3, ··· , n . Otra vez resulta que todos los ck son positivos y si son todos iguales, el resultado es claro. Supondremos, entonces que no todos son iguales entre sí. A causa del resultado anterior, se obtiene: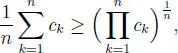
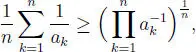
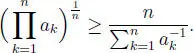
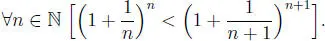
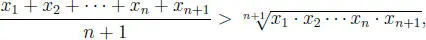
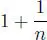 , xn + 1= 1 se obtiene:
, xn + 1= 1 se obtiene: