(6) ∀ n ∈  ( n = 1 ∨ ∃ m ∈
( n = 1 ∨ ∃ m ∈  ( s ( m ) = n )).
( s ( m ) = n )).
Demostración:
Sólo entregaremos la demostración de (3). Pues bien, sea A = { n ∈  | n > 0}, haremos ver que A es inductivo.
| n > 0}, haremos ver que A es inductivo.
En primer lugar, 1 ∈ A , pues sabemos que 1 > 0, esto es a causa de la axiomática de que ( 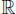 , +, ·, ≤) es campo ordenado. Por otra parte, sea n ∈ A , entonces n ∈
, +, ·, ≤) es campo ordenado. Por otra parte, sea n ∈ A , entonces n ∈  y n > 0, luego ( n + 1) ∈
y n > 0, luego ( n + 1) ∈  y como n + 1 > 1 > 0 se concluye que ( n + 1) ∈ A .
y como n + 1 > 1 > 0 se concluye que ( n + 1) ∈ A .
Por lo tanto, tenemos que A es inductivo, en consecuencia, resulta  ⊆ A , o sea, ∀ n ∈
⊆ A , o sea, ∀ n ∈  (n > 0).
(n > 0).
Nota:
El esquema que se utilizó en la demostración anterior es el siguiente:
(1) Se construye el conjunto A = { n ∈  | n satisface la propiedad p }, lo que simbolizamos mediante A = { n ∈
| n satisface la propiedad p }, lo que simbolizamos mediante A = { n ∈  | p ( n )}.
| p ( n )}.
(2) Se demuestra que el conjunto A definido en (1) es inductivo, es decir:
(2.1) 1 ∈ A , lo que es equivalente a demostrar que 1 tiene la propiedad p , es decir p (1).
(2.2) n ∈ A s ( n ) ∈ A , o sea si n ∈ A , entonces p ( n ) → p ( n + 1).
(2.3) Se concluye que  ⊆ A , o sea, ∀ n ∈
⊆ A , o sea, ∀ n ∈  (p(n) .
(p(n) .
El esquema anterior es lo que se conoce como Primer principio de inducción matemática, este principio nos entrega un metodo para demostrar cualquier propiedad p ( n ) para todos los números naturales.
1.2 Principios de inducción
1.2.1 Primer principio de inducción
El enunciado de este principio es el siguiente:
Sea p ( n ) una formula en n , entonces:
[ p (1) ∧ ∀ n ∈  ( p ( n ) → p(n + 1))] → ∀ n ∈
( p ( n ) → p(n + 1))] → ∀ n ∈  ( p ( n )).
( p ( n )).
Nota:
Tenemos:
2 + 4 + 6 + ⋯ 2 n = 2(1 + 2 + 3 + ⋯ + n ),
ahora bien, veremos en el problema resuelto [1.3.2] que:
1 + 2 + 3 + ⋯ + n = 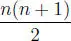 ,
,
con lo que:
2 + 4 + 6 + ⋯ + 2 n = 2(1 + 2 + 3 + ⋯ + n ) = 2 · 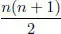 = n ( n + 1) = n 2+ n ≠ n 2+ n + 1,
= n ( n + 1) = n 2+ n ≠ n 2+ n + 1,
sin embargo, si consideramos la proposición falsa:
2 + 4 + 6 + ⋯ + 2 n = n 2+ n + 1,
como verdadera para n , sumando (2 n + 2) a cada lado de ésta, se cumple que:
2 + 4 + 6 + ⋯ + 2 n + (2 n + 2) = n 2+ n + 1 + (2 n + 2) =
= n 2+ 2 n + 1 + n + 1 + 1 = ( n + 1) 2+ ( n + 1) + 1,
vemos que se satisface la hipótesis inductiva. No se puede tener la igualdad para un primer n , por ejemplo, para 1, 2, etc.
Al no cumplirse para n = 1, 2, 3, · · · no podemos concluir que es falsa, pues podría ser verdadera por ejemplo para n = 2789341.
Nota:
El siguiente resultado es equivalente con el primer principio de induccióny proposición el metodo para resolver aquellos casos en que se desea demostrar inductivamente una propiedad p ( n ) no necesariamente para todo natural n , sino que para aquellos n mayores o iguales a algún natural a .
Teorema 1.2.1 Sea n 0∈  , p ( n ) una fórmula que contiene a n, entonces:
, p ( n ) una fórmula que contiene a n, entonces:
[ p ( n 0) ∧ ∀ n ∈  (( n ≥ n 0∧ p ( n ) → p ( n + 1))] → ∀ n ∈
(( n ≥ n 0∧ p ( n ) → p ( n + 1))] → ∀ n ∈  ( n ≥ n 0) p ( n ).
( n ≥ n 0) p ( n ).
Demostración:
Si n 0= 1 se tiene el primer principio de inducciony el teorema es cierto. Consideremos, entonces para n 0∈  el conjunto:
el conjunto:
I 1= { n ∈  | ( n ≥ n 0→ p ( n )} .
| ( n ≥ n 0→ p ( n )} .
Haremos ver que I 1es un conjunto inductivo.
En primer lugar, tenemos que 1 ∈ I 1puesto que:
(i) Si 1 ≥ n 0, entonces n 0= 1 y, por hipótesis, se tiene que p ( n 0) es verdad, luego, p (1) es verdadero y 1 ∈ I 1.
(ii) Si 1 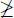 n 0, entonces 1 ≥ n 0→ p (1) es verdad, porque el antecedente es falso, luego 1 ∈ I 1.
n 0, entonces 1 ≥ n 0→ p (1) es verdad, porque el antecedente es falso, luego 1 ∈ I 1.
Tomemos ahora n ∈ I 1, entonces n ∈  y n ≥ n 0→ p(n), luego tenemos que (n + 1) ∈
y n ≥ n 0→ p(n), luego tenemos que (n + 1) ∈  y se presentan dos casos:
y se presentan dos casos:
Читать дальше

 ( n = 1 ∨ ∃ m ∈
( n = 1 ∨ ∃ m ∈  , +, ·, ≤) es campo ordenado. Por otra parte, sea n ∈ A , entonces n ∈
, +, ·, ≤) es campo ordenado. Por otra parte, sea n ∈ A , entonces n ∈ 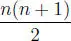 ,
,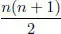 = n ( n + 1) = n 2+ n ≠ n 2+ n + 1,
= n ( n + 1) = n 2+ n ≠ n 2+ n + 1, n 0, entonces 1 ≥ n 0→ p (1) es verdad, porque el antecedente es falso, luego 1 ∈ I 1.
n 0, entonces 1 ≥ n 0→ p (1) es verdad, porque el antecedente es falso, luego 1 ∈ I 1.










