7.2.2 La unidad imaginaria
7.2.3 La conjugacion compleja
7.2.4 Modulo de un complejo
7.3 Forma polar de un número complejo
7.4 Raíces de un número complejo
7.4.1 Raíces cuadradas de z 0
7.4.2 Raíces n-esimas de
7.5 Gráficos elementales. Multiplicacion de un complejo por un complejo unitario
7.5.1 Grúaficos elementales
7.5.2 Complejo por complejo unitario
7.6 La recta y la circunferencia en el plano complejo
7.6.1 Ecuacion de la recta
7.6.2 Ecuacion de la circunferencia
7.7 Simetral de un trazo. Circunferencia de Apolonio
7.7.1 Simetral de un trazo
7.7.2 Circunferencia de Apolonio
7.8 Argumento de un trazo dirigido y úangulo entre trazos dirigidos
7.8.1 Trazo dirigido
7.8.2 Ángulo entre trazos
7.9 Arco capaz de y con cuerda AB
7.10 Problemas resueltos
7.11 Problemas propuestos
7.12 Respuestas a los problemas propuestos
Capitulo 8 Polinomios y ecuaciones
8.1 Series formales
8.2 Polinomios
8.2.1 Metodo de división sintetica
8.2.2 Maximo común divisor entre dos polinomios
8.2.3 Evaluacion de polinomios
8.2.4 Resultados clúasicos
8.2.6 Relacion entre raíces y coeficientes
8.3 Ecuaciones
8.3.1 Transformacion de ecuaciones
8.3.2 Ecuaciones recúprocas
8.3.3 La ecuaciún cúbica
8.4 Problemas propuestos
8.5 Respuestas a los problemas propuestos
Bibliografía
Capítulo 1
NÚMEROS NATURALES
En la presentación efectuada en la enseñanza media, se introdujeron los números reales. Este conjunto no vacío, que se simbolizo por 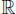 , satisface la axiomatica de campo ordenado y completo. Los elementos de este conjunto pasaron a ser los números reales y ayudados por la teoría de conjuntos se definieron algunos conjuntos de números reales tales como los naturales
, satisface la axiomatica de campo ordenado y completo. Los elementos de este conjunto pasaron a ser los números reales y ayudados por la teoría de conjuntos se definieron algunos conjuntos de números reales tales como los naturales  , los enteros
, los enteros 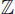 , los racionales
, los racionales 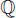 , los irracionales
, los irracionales 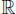 —
— 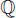 , o sea partimos del conjunto universo
, o sea partimos del conjunto universo 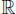 y fuimos consiguiendo subconjuntos de
y fuimos consiguiendo subconjuntos de 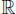 hasta obtener
hasta obtener  . La pregunta que se plantea es: ¿Se podra proceder al reves, es decir, partir de
. La pregunta que se plantea es: ¿Se podra proceder al reves, es decir, partir de  y llegar a
y llegar a 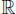 ? Este camino es posible, pero requiere de una mayor conceptualizaciúon.
? Este camino es posible, pero requiere de una mayor conceptualizaciúon.
1.1 Conjuntos inductivos
Definición 1.1.1 Sea A un conjunto de números reales, entonces:
A es inductivo  (1 ∈ A ∧ ∀ x ∈
(1 ∈ A ∧ ∀ x ∈ 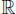 ( x ∈ A → ( x + 1) ∈ A )).
( x ∈ A → ( x + 1) ∈ A )).
Notas:
Hacemos ver que si A es inductivo, entonces 1 ∈ A , (1 + 1) = 2 ∈ A , tambien 2 + 1 = 3 ∈ A , etc.
Algunos ejemplos de conjuntos inductivos son 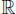 ,
, 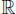 +, { x | x ≥ 1},
+, { x | x ≥ 1}, 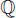 ,
, 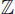 , etc.
, etc.
Como ejemplos de conjuntos no inductivos tenemos 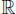 −, [ − 3, 8, ( − 13, 81], { x | x ≤ 1}, etc.
−, [ − 3, 8, ( − 13, 81], { x | x ≤ 1}, etc.
Definición 1.1.2 El conjunto de los números naturales se define como:
 = { x ∈
= { x ∈ 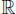 | para todo conjunto A inductivo; x ∈ A }.
| para todo conjunto A inductivo; x ∈ A }.
Nota:
La definición anterior nos dice que  es el menor conjunto de números reales que es inductivo.
es el menor conjunto de números reales que es inductivo.
Haremos ver que  contiene exactamente a los números:
contiene exactamente a los números:
1, 2, 3, 4, ⋯ , n , ( n + 1), ⋯
Por tal motivo deberemos entregar la definición de función sucesor.
Definición 1.1.3 La función sucesor s : 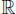 →
→ 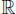 se define por s ( x ) = x + 1.
se define por s ( x ) = x + 1.
El objetivo principal al entregar la definición anterior es para que el teorema que viene a continuacion quede bien expresado.
Teorema 1.1.1 Se tiene:
(1) ∈  .
.
(2) ∀ n ∈  ( s ( n ) ∈
( s ( n ) ∈  ).
).
(3) ∀ n ∈  ( n > 0).
( n > 0).
(4) ∀ n ∈  ( s ( n ) ≠ 1).
( s ( n ) ≠ 1).
(5) ∀ n ∈  ∀ m ∈
∀ m ∈  ( s ( n ) = s ( m ) → n = m ).
( s ( n ) = s ( m ) → n = m ).
Читать дальше

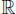 , satisface la axiomatica de campo ordenado y completo. Los elementos de este conjunto pasaron a ser los números reales y ayudados por la teoría de conjuntos se definieron algunos conjuntos de números reales tales como los naturales
, satisface la axiomatica de campo ordenado y completo. Los elementos de este conjunto pasaron a ser los números reales y ayudados por la teoría de conjuntos se definieron algunos conjuntos de números reales tales como los naturales  , los enteros
, los enteros 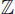 , los racionales
, los racionales 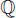 , los irracionales
, los irracionales  (1 ∈ A ∧ ∀ x ∈
(1 ∈ A ∧ ∀ x ∈ 










