ESTRUCTURAS DE ÁLGEBRA MULTILINEAL
Educació. Materials 16
Joaquín Olivert Pellicer
ESTRUCTURAS DE ÁLGEBRA MULTILINEAL
UNIVERSITAT DE VALÈNCIA 1996
Col·lecció: Educació. Materials
Director de la col·lecció: Guillermo Quintás Alonso
Joaquín Olivert Pellicer, doctor en Ciències Físiques, és professor titular de Física Teòrica de la Universitat de València.
© El autor, 1996
© D'aquesta edició: Universitat de València, 1996
| Disseny original de la coberta: |
Clemente Miranda Mora |
| Fotocomposició i maquetació: |
Servei de Publicacions |
|
Universitat de València |
ISBN: 978-84-370-9416-8
Dipòsit legal: V-2533-1996
| Impressió: |
GUADA Litografía, S.L. |
|
Camí Nou de Picanya, 3 |
|
46014 - València |
Índice
PRÓLOGO
PREÁMBULO
PARTE I: TEORÍA DE CONJUNTOS Y CARDINALIDAD
Capítulo 1. Axiomática
1.1 Clases y conjuntos
1.2 Subconjuntos
1.3 Singuletes y pares ordenados
1.4 Relaciones binarias
1.5 Aplicaciones o funciones
1.6 Producto cartesiano y leyes de composición
1.7 Relaciones de equivalencia
Capítulo 2. El axioma de elección
2.1 Buena ordenación
2.2 Ordinales y números ordinales
2.3 Axioma de elección. Proposiciones equivalentes
Capítulo 3. Cardinalidad
3.1 Números naturales
3.2 Números cardinales
3.3 Conjuntos finitos e infinitos
3.4 Operaciones con cardinales. Propiedades de los números transfinitos
3.5 Hipótesis del continuo
Capítulo 4. Aplicaciones en estructuras algebraicas
4.1 Aplicaciones en relaciones de equivalencia
4.2 Estructuras algebraicas
4.3 Homomorfismos de grupos
4.4 Construcción de los números enteros y racionales
Capítulo 5. Conjuntos ordenados
5.1 Ordenación en los números naturales. Caracterización
5.2 Relación de orden en el conjunto de los números enteros
5.3 Extensión de la relación de orden a los racionales
5.4 Propiedades arquimedianas de los números enteros y racionales. Algoritmo de la división
5.5 Operaciones con desigualdades
5.6 Forma decimal de los números racionales
Capítulo 6. Álgebra de ideales
6.1 Anillos de integridad
6.2 Máximo común divisor. Teorema de Bezout
6.3 Fracciones continuas. Resolución de la ecuación diofántica lineal
6.4 Teorema Chino del resto
6.5 Anillos de polinomios
6.6 Aplicación a los cuerpos 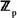
Capítulo 7. El número real
7.1 Sucesiones en 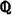
7.2 Sucesiones de Cauchy
7.3 Construcción de los números reales
7.4 Valor absoluto de un número real. Propiedades
7.5 Convergencia de sucesiones de Cauchy en 
7.6 Los números complejos
7.7 Cardinalidad de  y de
y de 
PARTE II: OPERACIONES CON MÓDULOS
Capítulo 8. Módulos
8.1 Módulos de A-homomorfismos
8.2 Producto, coproducto y suma directa de A-módulos
8.3 Módulos libres
Capítulo 9. Sucesiones exactas de homomorfismos de módulos
9.1 Sucesiones exactas de módulos
9.2 Teoremas de isomorfía
9.3 Módulos proyectivos
Capítulo 10. Producto tensorial
10.1 Definición y existencia
10.2 Bimódulos
10.3 Producto tensorial de homomorfismos de módulos
Capítulo 11. Álgebra tensorial
11.1 Definición y existencia
11.2 Grupos de permutaciones
11.3 A-homomorfismos inducidos por permutaciones
Capítulo 12. Producto exterior
12.1 Potencias exteriores
12.2 Álgebra exterior
PARTE III: TENSORES. FORMAS EXTERIORES
Capítulo 13. Espacios vectoriales
13.1 Concepto de dimensión
13.2 Teoremas de la dimensión
13.3 Espacio vectorial de homomorfismos. Espacios duales
Capítulo 14. Espacios tensoriales
14.1 Producto tensorial de módulos libres
14.2 Producto tensorial de espacios vectoriales
14.3 Aplicaciones
14.3.1 Complexificación de espacios vectoriales reales
14.3.2 Tensores
Capítulo 15. Formas exteriores
15.1 Dimensión de potencias exteriores de espacios vectoriales. Componentes estrictas
15.2 Álgebra de formas multilineales. Antisimetrización
15.3 Álgebra de Grassmann
15.4 Determinantes de un endomorfismo
Capítulo 16. Espacios simplécticos
16.1 Formas bilineales degeneradas
16.2 Espacios vectoriales presimplécticos
16.3 Espacios vectoriales simplécticos. Grupos simplécticos
PARTE IV: PRODUCTOS ESCALARES. MÉTRICAS
Capítulo 17. Formas hermíticas
17.1 Definición y propiedades inmediatas. Formas hermíticas positivas.
17.2 Método de ortonormalización de Gram-Schmidt
17.3 Espacios euclídeos
17.4 Ley de ascenso y descenso de índices
Capítulo 18. Operadores normales
18.1 Vectores y valores propios de endomorfismos
18.2 Operadores adjuntos en espacios prehilbertianos
18.3 Operadores normales
18.4 Operadores hermíticos y unitarios
18.5 Extensiones a los espacios complexificados
18.6 Operadores normales en espacios euclídeos
18.7 Isometrías en espacios euclídeos
Capítulo 19. Formas canónicas de matrices
19.1 Polinomio característico
19.2 Teorema de Cayley-Hamilton
19.3 Endomorfismos nilpotentes
19.4 Subespacios invariantes. Nilpotencias parciales. Ecuación minimal
19.5 Teorema de Jordan-Che valley. Consecuencias
19.6 Determinación del polinomio característico. Método de Fadeev.
Capítulo 20. Formas cuadráticas
20.1 Método de resolución de Gauss
20.2 Descomposición de una matriz cuadrada en producto de matrices triangulares
20.3 Determinación de la matriz inversa
20.4 Signatura de una forma cuadrática
20.5 Reducción de una forma cuadrática por el método de Jacobi
20.6 Reducción de una forma cuadrática por el método de Lagrange
20.7 Clasificación de cónicas (no degeneradas)
Capítulo 21. Productos tensoriales de álgebras asociativas
21.1 Aplicación de estructura. Producto tensorial canónico
21.2 Módulos, anillos y álgebras graduadas
21.3 Producto tensorial anticonmutativo de álgebras G-graduadas
21.4 Involuciones y antiderivaciones
Capítulo 22. Productos escalares de álgebras tensoriales y exteriores.
22.1 Núcleos de productos tensoriales de aplicaciones lineales
22.2 Productos escalares en el álgebra tensorial
22.3 Producto escalar en el álgebra exterior
Читать дальше