Definición 3.9: Una clase Xx se dice que está parcialmente ordenada respecto a la relación binaria si x y e y z, entonces x z.
Es decir que sólo se exige que la relación binaria posea la Propiedad transitiva.En realidad, de acuerdo con el Teorema de la buena ordenación, todo conjunto admite un buen orden respecto a la relación de orden definida en el Teorema 3.3.Para esta relación todo conjunto está parcialmente ordenado; pero puede suceder que no lo sea para otro tipo de relaciones binarias.
Definición 3.10: Sea A un subconjunto de un conjunto X parcialmente ordenado con la relación binaria . Se dice que c X es cota superior de A si y 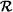 c para todo y
c para todo y  A. Y se dirá que c es cota inferior de A si c
A. Y se dirá que c es cota inferior de A si c 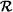 y para todo y
y para todo y  A. La menor de las cotas superiores de un conjunto se ¡lama supremo, y la mayor de las cotas inferiores es llamada ínfimo.
A. La menor de las cotas superiores de un conjunto se ¡lama supremo, y la mayor de las cotas inferiores es llamada ínfimo.
Un elemento m  A se dirá que es maximal si no existe ningún elemento y
A se dirá que es maximal si no existe ningún elemento y  A que verifique que m
A que verifique que m 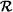 y. Y se dirá minimal si tampoco existe un y
y. Y se dirá minimal si tampoco existe un y  A tal que y
A tal que y 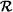 m.
m.
Definición 3.11: Sea X un conjunto parcialmente ordenado con la relación de orden . Se dice que X es un conjunto inductivo (o inductivamente ordenado) si toda cadena posee una cota superior.
Con estas nuevas definiciones, prosigamos estudiando consecuencias del Axioma de eleccióny sus equivalencias.
Teorema 3.12: (Lema de Zorn) Todo conjunto inductivo posee un elemento maximal. Demostración :
Sea X un conjunto inductivamente ordenado por una relación de orden . Para cada a x definimos

y con Xa , construimos S = {X a:a  x }.
x }.
La aplicación

es biyectiva y conserva el orden, es decir,

Esto implica que S es inductivo con la relación de inclusión C, luego en virtud del Teorema 3.8 posee un elemento maximal, y por lo tanto X también lo tiene.
Teorema 3.13: Todo elemento de un conjunto inductivamente ordenado precede a un elemento maximal. Demostración :
Sea A un conjunto inductivamente ordenado y tomemos u  A. Formemos la siguiente clase
A. Formemos la siguiente clase
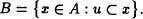
Evidentemente B A. Luego en virtud del Teorema 2.1 del Capítulo 1 B es conjunto, que obviamente es inductivo. Por el Lema de Zorn, B posee un elemento maximal m que también es maximal en A. En consecuencia, u m.
Podría suceder que u fuese maximal en A. Dado que u u , résulta que u precede a sí mismo.
Teorema 3.14: El Teorema 3.13 induce el Axioma de elección de Zer- melo.
Demostración :
Sea X un conjunto no vacío arbitrario, y sobre él formemos la clase A de funciones de elección definidas sobre subconjuntos de X. Esta clase es no vacía, pues los subconjuntos de la forma {x} tienen por función de elección la definida por F({z}) = x . En virtud de la Proposición 6.5 del Capítulo 1 A es conjunto por ser subclase de P(X)X , ya que si X es conjunto, P(X) es conjunto (Teorema 2.7 del mismo capítulo).
Establezcamos en A un orden parcial: Dadas f,g A, diremos que f  g si y sólo si def f
g si y sólo si def f  def g y g |def f = f . Claramente esta relación tiene la Propiedad transitiva.
def g y g |def f = f . Claramente esta relación tiene la Propiedad transitiva.
Veamos que A es inductivo :
Consideremos una cadena {f i} arbitraria de A y hemos de encontrar una cota superior. Para ello construimos la aplicación

Evidentemente es cota superior de la cadena. Luego A es inductivo.
Al ser A inductivo, podemos tomar un elemento maximal h de A que seguirá siendo una función de elección sobre subconjuntos de X. Puede suceder que def h — p(X ), o que exista un elemento no vacío (subconjunto de X) u  ‘P(X) ~ def h. Si ocurre el primer caso, se tiene ya el Axioma de Zermelo.En caso contrario, tomemos un elemento v u; y definamos la función h {(u, v)} que es una función de elección sobre def h {u} . En consecuencia, h no sería element maximal.
‘P(X) ~ def h. Si ocurre el primer caso, se tiene ya el Axioma de Zermelo.En caso contrario, tomemos un elemento v u; y definamos la función h {(u, v)} que es una función de elección sobre def h {u} . En consecuencia, h no sería element maximal.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

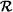 c para todo y
c para todo y  A. Y se dirá que c es cota inferior de A si c
A. Y se dirá que c es cota inferior de A si c 


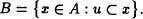
 g si y sólo si def f
g si y sólo si def f 











