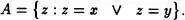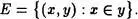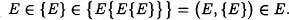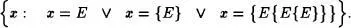Esto es evidente debido a que def f es unión de 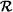 -secciones de tipo def g e Im f es unión de «S-secciones Im g.
-secciones de tipo def g e Im f es unión de «S-secciones Im g.
Probemos quedef f = X ó Im f = Y :
Si no lo son, existe un 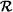 - primer elemento it de X ~ def f y un
- primer elemento it de X ~ def f y un 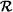 -imprimer elemento v de Y ~ Im f. Entonces la función f ⋃ {(u, v)} también conserva el orden - S. Luego existe un g de manera que ( u, v )
-imprimer elemento v de Y ~ Im f. Entonces la función f ⋃ {(u, v)} también conserva el orden - S. Luego existe un g de manera que ( u, v )  g , y, por definición de f, se tiene que
g , y, por definición de f, se tiene que  f.
f.
Podemos repetir el razonamiento hasta llegar a que def f = X ó Im f = Y.
Corolario 1.14: Si H ordena bien a X y S ordena bien a Y, de manera que X sea un conjunto e Y una clase propia, existe una función f que conserva el orden -S de manera que def f = X . Demostración :
Está claro que no se puede verificar que Im f = Y , ya que Im f es conjunto e Y clase propia. Esto hace que, según el Teorema1.13, def f = X.
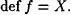
2.2 Ordinales y números ordinales
Entre las clases bien ordenadas, la clase de los números ordinales es un ejemplo de ellas. En esta Sección nos dedicaremos a construir esta clase, y para ello definiremos el concepto de ordinal con sus propiedades más características.
Empecemos introduciendo un nuevo axioma :
VII Axioma de regularidad
Si x ≠ 0, existe un elemento y x que verifica
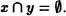
El enunciado de este axioma puede prestarse a confusión en el sentido de que podría pensarse que x ⋂ y = y, en vez de x ⋂ {y} = {y} que simpre es cierta. Efectivamente, x ⋂ y está formado por los elementos comunes de x y de y. El axioma anterior precisamente exige que al menos un elemento de x no tenga elementos comunes con x.
Consecuencias inmediatas de este axioma son :
Proposición 2.1: x ≠ x .
Demostración :
Lo probaremos por reducción al absurdo :
Consideremos que x  x , entonces x es un conjunto no vacío, y por tanto es, a su vez, el único elemento de {x}, es decir, y = x. Ahora bien, por el último axioma, existe un y
x , entonces x es un conjunto no vacío, y por tanto es, a su vez, el único elemento de {x}, es decir, y = x. Ahora bien, por el último axioma, existe un y  {x} tal que
{x} tal que
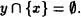
Pero este resultado contradice el hecho que y  y
y  {x}.
{x}.
Ahora estamos en condiciones de aceptar como válida la posible intuición (que seguramente tuvo el lector al leer la introducción del capítulo anterior) de que ningún conjunto es elemento de sí mismo. Esta intuición es una verdad lógica si aceptamos el Axioma de regularidad.En estas circunstacias, la clase de Russell R coincide con la clase universal 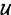 .
.
Proposición2.2: Es falso que x y ∧ y x.
Demostración :
Consideremos que x  y, y
y, y  x. En consecuencia, x, y son conjuntos, y son los únicos elementos de la clase
x. En consecuencia, x, y son conjuntos, y son los únicos elementos de la clase
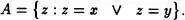
Aplicando el Axioma de regularidad, se llega a una contradicción, ya que ningún elemento de A posee intersección vacía con la clase A.
Definición 2.3:Se llama clase E la clase de pares ordenados
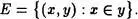
De esta misma definición, se desprende que E es una relación binaria, que posee la Propiedad asimétrica.
Teorema 2.4: La clase E es propia.
Demostración :
Consideremos que E sea conjunto, es decir, E 
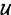 ; entonces {E}
; entonces {E}  y (E,{E})
y (E,{E})  E (ya que E
E (ya que E  {-E}). En virtud de la definición de par ordenado (Definición 3.7del Capítulo 1), (E, {E} ) = { E{ E{ E}}} , con lo que
{-E}). En virtud de la definición de par ordenado (Definición 3.7del Capítulo 1), (E, {E} ) = { E{ E{ E}}} , con lo que
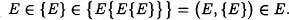
Construyamos la clase
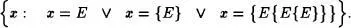
Pero esta clase contradice el Axioma de regularidad, lo que es absurdo y, por tanto, E no es un conjunto.
Estudiada la clase E, podemos ocuparnos ampliamente del concepto de ordinal a partir de una definición previa.
Definición 2.5: Una clase x se dice que es o está saturada (o completa) si y sólo si cada elemento de x es un subconjunto propio de x (es decir, un subconjunto distinto de x).
Definición 2.6: x es un ordinal si x es una clase saturada y E conecta a x
Analicemos detenidamente este concepto: Por definición de E resulta que, dados dos elementos distintos de x, uno es elemento del otro. Además, los elementos de los miembros de x son elementos de x (Condición de saturación de una clase), lo que dota a E de la Propiedad transitivaen x.
Читать дальше

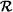 -secciones de tipo def g e Im f es unión de «S-secciones Im g.
-secciones de tipo def g e Im f es unión de «S-secciones Im g. g , y, por definición de f, se tiene que
g , y, por definición de f, se tiene que 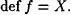
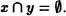
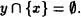
 {x}.
{x}. .
.