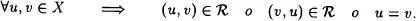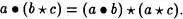
En la práctica no se ponen los paréntesis que aparecen en el segundo miembro, ya que se sobreentiende que el elemento a actúa por separado sobre los elementos b, c mediante la ley •, y luego los resultados se componen con la ley *
En cuanto a las leyes de composición externas sólo expondremos la definición, pues sus propiedades se irán introduciendo en los casos en que aparezcan :
Definición 6.14:Consideremos C y D dos conjuntos. Una ley de composición externa de D sobre C es toda aplicación
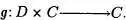
1.7 Relación de equivalencia
Definición 7.1: Una relación binaria S es una relación de equivalencia si posee las propiedades reflexiva, simétrica y transitiva.
Para expresar que dos elementos a y b pertenecen a la relación de equivalencia 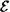 , (a,b)
, (a,b) 
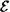 , se emplea la notación
, se emplea la notación
y se lee “a (es) equivalente a b”. También escribiremos
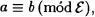
que se lee “a congruente con (o equivalente a) b mòdulo e”.
Definición 7.2: Se llama clase de equivalencia de un elemento b a la clase formada por los elementos equivalentes a b.
Proposición 7.3: Sea C(a) la clase de equivalencia de a. Dos elementos arbitrarios b y c de C(a) son equivalentes.
Demostración :
Por ser b equivalente a a,b a , y por ser c equivalente a a, c£ a. En virtud de la Propiedad simétrica, a c . Y la Propiedad transitiva hace que b c . Luego b y c son equivalentes.
Proposición 7.4: Dos clases de equivalencia que tengan un elemento común son iguales.
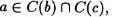
Demostración :
Sea
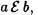
y elijamos un 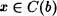 . Entonce x£ a , y debido a que a£ c , se tiene por la Propiedad transitiva que x c . Luego
. Entonce x£ a , y debido a que a£ c , se tiene por la Propiedad transitiva que x c . Luego 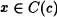 . De igual forma se prueba que los elementos de C(c) son elementos de C(b). Por el Axioma de extensión,
. De igual forma se prueba que los elementos de C(c) son elementos de C(b). Por el Axioma de extensión,
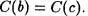
Definición 7.5: Consideremos una relación de equivalencia en C. Se llama clase cociente a la clase formada por las clases de equivalencia de , y se representa por .
Entre C y 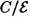 existe una aplicación /i, llamada proyección canónica, definida por
existe una aplicación /i, llamada proyección canónica, definida por

Evidentemente esta aplicación es suprayectiva.
Proposición 7.6: Si es conjunto, es conjunto .
Demostración :
Debido a que  es suprayectiva,
es suprayectiva,
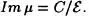
Ahora bien, dado que def 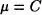 , por el Axiomade sustitución,
, por el Axiomade sustitución, 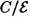 es conjunto.
es conjunto.
Es frecuente en un principiante confundir 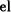 conjunto de clases de equivalencia (conjunto cociente) con la unión de estas mismas clases de equivalencia. Para salir del error, pensemos de nuevo en el símil de los pueblos.
conjunto de clases de equivalencia (conjunto cociente) con la unión de estas mismas clases de equivalencia. Para salir del error, pensemos de nuevo en el símil de los pueblos.
Establezcamos en una nación una relación binaria que consiste que dos individuos estén relacionados si se hallan empadronados en un mismo centro. Está claro que esta relación es de equivalencia. Sus clases de equivalencia formarán los pueblos que integran la nación. La unión de todos los pueblos será esta misma nación. En cambio, el conjunto cociente resulta ser la ¡Federación de pueblos! , que, desde luego, es totalmente distinta a la unión.
1 El Teorema de Incompletitud de Godei asegura que todo sistema lógico es incompleto. Esto quiere decir que simpre habrá proposiciones que no podrán ser confirmadas ni negadas en el marco del cuerpo axiomático en que se trabaja: proposiciones indecidibles. Si se tuviera una Teoría de Conjuntos completa, ésta no sería lógica, pues sería incompatible con el Teorema de Incompletitud, por lo que contendría contradiciones entre sus proposiciones.
2. El axioma de elección
Continuando con la construcción de una teoría de conjuntos, abordamos en este Capítulo el Axioma de elección.Quizá es el axioma más controvertido de la axiomática conjuntista, pues históricamente no ha sido aceptado por todas las escuelas de matemáticos. Por ello, los partidarios del mismo se han esforzado en buscar equivalencias con otras proposiciones que en otros sistemas lógicos se consideran como puntos de partida.
Con el fin de obtener una clara exposición sobre este particular, desarrollamos el concepto de la buena ordenación que poseen los conjuntos y que ya Cantor lo había utilizado en sus primeros trabajos sobre los números transfinitos. Luego abordaremos el concepto de ordinal y de número ordinal. Se probará que la clase de los números ordinales es propia y goza de una buena ordenación. Ello nos servirá para obtener consecuencias equivalentes del Axioma de elecciónya citado, y que abordaremos en la última Sección de este Capítulo.Pero los ordinales también serán utilizados en el siguiente capítulo para construir los números naturales y los cardinales en general.
2.1 Buena ordenación
Definición 1.1: Sea R una relación binaria. Se dice que R conecta a X si y sólo si
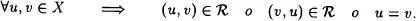
Se dice que z es un R-primer elemento de X si y sólo si z X y dado y X, con y ≠ z, es falso que (y, z) R.
Читать дальше

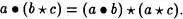
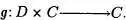
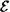 , (a,b)
, (a,b) 
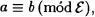
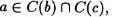
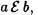
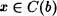 . Entonce x£ a , y debido a que a£ c , se tiene por la Propiedad transitiva que x c . Luego
. Entonce x£ a , y debido a que a£ c , se tiene por la Propiedad transitiva que x c . Luego 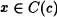 . De igual forma se prueba que los elementos de C(c) son elementos de C(b). Por el Axioma de extensión,
. De igual forma se prueba que los elementos de C(c) son elementos de C(b). Por el Axioma de extensión,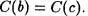
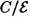 existe una aplicación /i, llamada proyección canónica, definida por
existe una aplicación /i, llamada proyección canónica, definida por
 es suprayectiva,
es suprayectiva,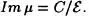
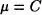 , por el Axiomade sustitución,
, por el Axiomade sustitución, 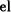 conjunto de clases de equivalencia (conjunto cociente) con la unión de estas mismas clases de equivalencia. Para salir del error, pensemos de nuevo en el símil de los pueblos.
conjunto de clases de equivalencia (conjunto cociente) con la unión de estas mismas clases de equivalencia. Para salir del error, pensemos de nuevo en el símil de los pueblos.