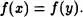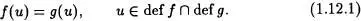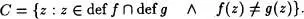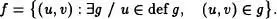Teorema 1.7: Si Y es una 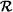 -sección de X con Y ≠ X, entonces existe un v
-sección de X con Y ≠ X, entonces existe un v  X de manera que
X de manera que
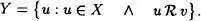
Demostración :
Sea y es una 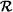 -sección de X que no coincide con X. Debido a que TZ ordena bien a X y X ~ Y X, la Definición 1.2asegura que X ~ Y posee ft-primer elemento v. Si consideramos que u £ X con u v , résulta que u X ~Y. Con ello se ha probado que
-sección de X que no coincide con X. Debido a que TZ ordena bien a X y X ~ Y X, la Definición 1.2asegura que X ~ Y posee ft-primer elemento v. Si consideramos que u £ X con u v , résulta que u X ~Y. Con ello se ha probado que
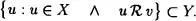
Tomemos u Y. Por ser Y 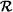 -sección, es falso que v u. Y como
-sección, es falso que v u. Y como 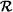 ordena bien a X, uv. Esto prueba la inclusion contraria.
ordena bien a X, uv. Esto prueba la inclusion contraria.
El siguiente resultado es inmediato por lo que lo damos sin ningún comentario :
Proposición 1.8: Dadas dos -secciones Y, Z de X, se verifica que Y Z ó Z Y.
Definición 1.9: Consideremos dos órdenes , S. Se dice que una aplicación f conserva el orden -S si 1Z ordena bien a def f y S ordena bien a Im f de manera que f(u) S f(v) si u v.
Teorema 1.10: Si ordena bien a X y f es una aplicación de una - sección Y en X, de manera que conserve el orden -, entonces es falso que f(u) u, ∀ u  Y .
Y .
Demostración :
Basta probar que
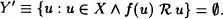
Supongamos que no lo sea. Entonces posee un ft-primer elemento v, que por pertenecer a Y', f(v) v; y al conservai / el orden, f(f{v)) f{v).
Si tomamos un u  X de manera que u v , resulta que u Y' (ya que v es un ft-primer elemento de y’), y por tanto, o u f(u), o u = f(u). Del mismo modo se tiene que f(v) Y' que conduce a que, o f(v)f (f(v)) , o f(v) = f (f(v)) , que resulta ser contradictorio con lo anterior. Esto hace que Y' =
X de manera que u v , resulta que u Y' (ya que v es un ft-primer elemento de y’), y por tanto, o u f(u), o u = f(u). Del mismo modo se tiene que f(v) Y' que conduce a que, o f(v)f (f(v)) , o f(v) = f (f(v)) , que resulta ser contradictorio con lo anterior. Esto hace que Y' = 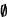 .
.
Teorema 1.11: Si f conserva el orden 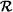 -S, entonces f es una aplicación inyectiva y f -1conserva el orden S-
-S, entonces f es una aplicación inyectiva y f -1conserva el orden S- 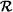 .
.
Demostración :
Tomemos
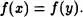
Entonces no puede verificarse por separado x y ni yx. En consecuencia, x = y.

Consideremos que f(u) S f(v). Entonces u ≠ v; y debido a que f conserva el orden - S, u v. Esto hace que f -1conserve el orden S - .
Teorema 1.12: Si f y g son aplicaciones de X en Y que conserven el orden - S , def f y def g son secciones de X, e Im f, Im g son secciones de Y, entonces f g ó g f.
Demostración :
Dado que def f , def y son secciones, la Proposición 1.8nos indica que, o def / C def y, o def y C def /. Y la demostración se reduce a probar que
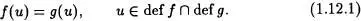
Definamos la clase
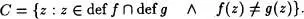
Si C es no vacía, tendrá un 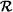 -primer elemento u, que verificará obviamente f(u) ≠ g(w). Supóngase que f(u) S g(u). Dado que Im g es una «S -sección de Y, f(u) Im g. (Recuérdese que no existen elementos fuera de las seciones que precedan a sus elementos). Luego existe un v X que verifique g(v) = f(u). Esto hace que g(v)Sg(u). Ahora bien, como y -1conserva el orden S- , resulta que vu. Pero u es el primer elemento de C en donde las aplicaciones difieren, lo que es una contradicción. Esto conduce a afirmar que C = 0, por lo tanto se cumple (1.12.1).
-primer elemento u, que verificará obviamente f(u) ≠ g(w). Supóngase que f(u) S g(u). Dado que Im g es una «S -sección de Y, f(u) Im g. (Recuérdese que no existen elementos fuera de las seciones que precedan a sus elementos). Luego existe un v X que verifique g(v) = f(u). Esto hace que g(v)Sg(u). Ahora bien, como y -1conserva el orden S- , resulta que vu. Pero u es el primer elemento de C en donde las aplicaciones difieren, lo que es una contradicción. Esto conduce a afirmar que C = 0, por lo tanto se cumple (1.12.1).
Teorema 1.13: Si ordena bien a X y S ordena bien a Y, existe una única función f que conserva el orden - S, tal que def f = X ó Im f = Y .
Demostración :
La cuestión que plantea el enunciado de este teorema no es la existencia de aplicaciones de X en Y que conserven el orden -S , pues estas funciones son fáciles de definir debido a que X e Y están bien ordenados, y se puede aprovechar esta circunstancia para ello. Además se construyen de manera que sus dominios de definición sean 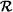 -secciones, y sus imágenes S -secciones. Pero eso no asegura que sus dominios sean X y sus imágenes Y. Representemos por g las aplicaciones de este tipo. El teorema prueba que existe una única aplicación cuyo dominio es X o su imagen, Y .
-secciones, y sus imágenes S -secciones. Pero eso no asegura que sus dominios sean X y sus imágenes Y. Representemos por g las aplicaciones de este tipo. El teorema prueba que existe una única aplicación cuyo dominio es X o su imagen, Y .
Definamos
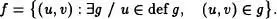
Esta relación binaria es una aplicación, ya que si existiesen dos aplicaciones g1, g2 con u  def g1 ⋂def g2 , el Teorema1.12 asegura que g 1(u) = g2{u).
def g1 ⋂def g2 , el Teorema1.12 asegura que g 1(u) = g2{u).
Veamos quedef f es una – sección e Im f es una S– sección :
Читать дальше

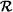 -sección de X con Y ≠ X, entonces existe un v
-sección de X con Y ≠ X, entonces existe un v  X de manera que
X de manera que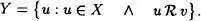
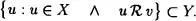
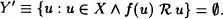
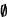 .
.