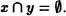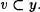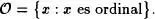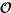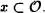Teorema 2.7: Si x es ordinal, E ordena bien a x.
Demostración :
Para que E ordene bien a x, tiene que conectarlo, hecho que por definición de ordinal ya se verifica. Además debe cumplir la Propiedad asimétricay que todo subconjunto posea un E -primer elemento, de acuerdo con la Definición 1.2.
Tomemos u,v x , de manera que u v , es decir, u £ v. Por la Proposición 2.2, es falso que v Eu. Luego la relación binaria E posee en x la Propiedad asimétrica.
Consideremos y un subconjunto no vacío de x. Por el Axioma de regularidad, y posee un elemento u tal que
es decir que ningún elemento de y pertenece au. En consecuencia, u es el E-p rimer elemento de y.
Proposición 2.8: Si x es un ordinal, y C x con y / x y de manera que y también sea saturado, entonces y x.
Demostración :
Basta probar que E conecta a y. Tomemos u E v, v E y. Por ser y saturado, u E y. Esto hace que y es una .E - sección de x. En virtud del Teorema 1.7, existe un w  x tal que
x tal que

Ahora bien, como cada elemento de w pertenece a x , resulta que
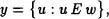
es decir, y = w , o lo que es lo mismo y x.
Nota 2.9: Este último teorema prueba que y es un ordinal, si tenemos en cuenta la Definición 2.6, ya que al estar x üJ-conectado y también lo está.
Proposición 2.10: Si x e y son ordinales, entonces x  y ó y
y ó y  x.
x.
Demostración :
Si x ey son iguales, se verifica trivialmente el teorema. Si son distintos, es obvio que la clase x  y está saturada, puesto que a; e y lo están. Por el teorema anterior, o x y = x, o x y x. El primer caso es equivalente a x
y está saturada, puesto que a; e y lo están. Por el teorema anterior, o x y = x, o x y x. El primer caso es equivalente a x  y. En cambio, si x y x , entonces x
y. En cambio, si x y x , entonces x  y (pues si cumpliese también x
y (pues si cumpliese también x  y
y  y, se verificaría x
y, se verificaría x  y
y  x
x  y, lo que contradice la Proposición 2.1). Ahora bien, como x
y, lo que contradice la Proposición 2.1). Ahora bien, como x  y es subconjunto de y e y es saturado, x
y es subconjunto de y e y es saturado, x  y debía ser elemento de y (y hemos visto que no lo es). La única posibilidad que queda es
y debía ser elemento de y (y hemos visto que no lo es). La única posibilidad que queda es
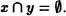
Corolario 2.11:Si x e y son ordinales, entonces, o x  y, o y
y, o y  x, o y = x.
x, o y = x.
Demostración :
Supongamos que sean distintos. Entonces la Proposición2.10 asegura que x  y o y
y o y  x. Ahora bien, como x e y están saturados y son distintos, aplicamos la Proposición2.8, con lo que, o x y , o y x.
x. Ahora bien, como x e y están saturados y son distintos, aplicamos la Proposición2.8, con lo que, o x y , o y x.
Teorema 2.12: Si x es un ordinal e y  x, entonces y es un ordinal. Demostración :
x, entonces y es un ordinal. Demostración :
Por ser x un ordinal, es saturado; y por tanto y x ( Definición 2.5). Esto hace que E también conecte a y.
Hemos de ver que y también es saturado :
Por de pronto, E conecta a y, puesto que E conecta a x. Ahora bien, dado que E es transitiva en x , también será transitiva en y. Por consiguiente, si tomamos un elemento v £ y y un elemento u v , por la Propiedad transitivade E, u y; es decir,
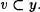
Luego y está saturado. En virtud de la Definición 2.6, y es un ordinal.
Definición 2.13:Representaremos la clase de los ordinales por
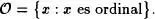
Teorema2.14: es una clase propia que es un ordinal. Demostración :
El Corolario2.11 y la Proposición2.12 muestran que E conecta 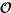
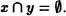
Tomemos un x arbitrario. Para cualquier elemento y x , será un ordinal en virtud del Teorema2.12, en consecuencia y . Luego
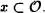
Con ello hemos probado que 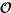 es saturado, y, por tanto, ordinal.
es saturado, y, por tanto, ordinal.
Finalmente, si 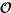 fuera conjunto,
fuera conjunto, 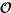

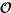 , lo que es absurdo en virtud de la Proposición 2.1.
, lo que es absurdo en virtud de la Proposición 2.1.
Читать дальше

 x tal que
x tal que
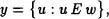
 y ó y
y ó y  y está saturada, puesto que a; e y lo están. Por el teorema anterior, o x y = x, o x y x. El primer caso es equivalente a x
y está saturada, puesto que a; e y lo están. Por el teorema anterior, o x y = x, o x y x. El primer caso es equivalente a x