Teorema 3.4: Si X es un conjunto cuyos elementos son conjuntos no vacíos disjuntos dos a dos, entonces existe un conjunto C que contiene exactamente un elemento de cada elemento de X.
Demostración :
Llamemos Y =  X. Por el Axioma de amalgamación, Y es un conjunto. Cada elemento u de X es un conjunto y, por el Corolario3.3, u está bien ordenado. Elijamos su primer elemento. Definimos una aplicación
X. Por el Axioma de amalgamación, Y es un conjunto. Cada elemento u de X es un conjunto y, por el Corolario3.3, u está bien ordenado. Elijamos su primer elemento. Definimos una aplicación 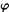 de manera que (u) sea el primer elemento de u , entonces
de manera que (u) sea el primer elemento de u , entonces
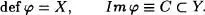
Y por el Teorema 2.1del Capítulo 1, C es conjunto.
Teorema 3.5: El Teorema 3-4 implica el axioma de Zermelo.
Demostración :
Sea X un conjunto, y definamos
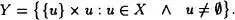
Obviamente existe una biyección entre X e Y , por lo que resulta que Y es conjunto, con la propiedad de que sus elementos son disjuntos dos a dos. En virtud del Teorema 3.4, construyamos la relación binaria
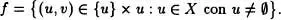
El mismo teorema prueba que para cada u existe un solo v , por lo que f es una función. Se obtiene de inmediato el Axioma de Zermelosi sustituimos X por P(X). En este caso f sería la función de elección.
Con estos teoremas estudiados, se ha puesto de manifiesto que el Axioma de elección de Zermelo, el Teorema de numerabili dad, el Teorema de la buena ordenación de Zermeloy la Proposición
3.4 son equivalentes. De hecho en muchas ocasiones algunos autores toman esta última proposición como el axioma de elección.
El Axioma de elección de Zermeloposee otras equivalencias que vamos a tratar. Se necesita otros conceptos como es el de cadena, el de elemento maximal y el de conjunto inductivo. El primero de ello se enuncia como :
Definición 3.6: Una clase k se dice que es una cadena si para x, y  k arbitrarios se verifica x ⊂ y ó y ⊂ x. Este concepto de cadena también se extiende para toda relación de orden arbitraria .
k arbitrarios se verifica x ⊂ y ó y ⊂ x. Este concepto de cadena también se extiende para toda relación de orden arbitraria .
Lema 3.7: Si k es una cadena y cada miembro de k es una cadena , k es una cadena.
Demostración :
Tomemos x, z 
 k . Existen m, p
k . Existen m, p  k tales que x m, z p . Por ser m, p elementos de la cadena k, m p ó p m. Supongamos que m
k tales que x m, z p . Por ser m, p elementos de la cadena k, m p ó p m. Supongamos que m  p. Entonces x
p. Entonces x  p , es decir, x, z
p , es decir, x, z  p , y al ser p cadena por hipótesis, x z ó z
p , y al ser p cadena por hipótesis, x z ó z  x. En virtud de la Definición 3.6,
x. En virtud de la Definición 3.6,  x es una cadena.
x es una cadena.
Principio maximal de Hausdorff
Teorema 3.8: Sea x un conjunto. Existe una cadena n tal que n ⊂ x, de manera que dada otra cadena m con m ⊂ x y n ⊂ m, se cumple n = m.
Demostración :
Para cada aplicación h definimos la clase
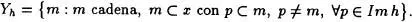
Evidentemente Yh es conjunto por verificar Yh ⊂ V(x). Tomemos una función F que satisfaga el Axioma de eleccióny definimos la aplicación g como
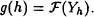
En virtud del Teorema 2.26, existe una función /, en la que def / es ordinal y que f(u ) = g(f|u) para todo ordinal u. Por definición de g , dado u  def f, f(u) = g(f|u) = F(Y fu) £ Y fu. Luego /(tt)es una cadena de x , y por tanto f(u ) ⊂ x.
def f, f(u) = g(f|u) = F(Y fu) £ Y fu. Luego /(tt)es una cadena de x , y por tanto f(u ) ⊂ x.
Tomemos u,v  def f distintos. Al ser u, v ordinales, uno es estrictamente mayor que el otro. Consideremos, por ejemplo, u < v; lo que es equivalente a que u v. Entonces f(u)
def f distintos. Al ser u, v ordinales, uno es estrictamente mayor que el otro. Consideremos, por ejemplo, u < v; lo que es equivalente a que u v. Entonces f(u)  f(v) , luego f(u) ≠ f(v) . Por consiguiente, F es inyectiva. Esto hace que f -1sea una aplicación. A partir de esta conclusion y puesto que X es conjunto, el Axioma de sustituciónasegura que Im f -1= def f es conjunto, es decir, un númro ordinal, esto hace que def f
f(v) , luego f(u) ≠ f(v) . Por consiguiente, F es inyectiva. Esto hace que f -1sea una aplicación. A partir de esta conclusion y puesto que X es conjunto, el Axioma de sustituciónasegura que Im f -1= def f es conjunto, es decir, un númro ordinal, esto hace que def f 
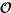 . lamemos n este ordinal. Con ello se obtiene que, puesto que def f
. lamemos n este ordinal. Con ello se obtiene que, puesto que def f  def f, n
def f, n  def f; y por tanto f(n) =
def f; y por tanto f(n) = 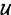 , es decir, g(f) = g(f|deî ) = . Pero esto contradice el hecho de que g(f) es un elemento de Y), o lo que es lo mismo g(f) no sería una cadena. Por consiguiente, no hay ninguna cadena contenida en x y que contenga propiamente a cada elemento de Imf. Ahora bien, por construcción de /, Im f es una cadena, y cada miembro de Im f es una cadena por ser imagen de un ordinal. Entonces, en virtud del Lema 3.7,
, es decir, g(f) = g(f|deî ) = . Pero esto contradice el hecho de que g(f) es un elemento de Y), o lo que es lo mismo g(f) no sería una cadena. Por consiguiente, no hay ninguna cadena contenida en x y que contenga propiamente a cada elemento de Imf. Ahora bien, por construcción de /, Im f es una cadena, y cada miembro de Im f es una cadena por ser imagen de un ordinal. Entonces, en virtud del Lema 3.7,  Im f es una cadena que contiene a todo elemento de Im f. Llamemos, pues, n = lm f.
Im f es una cadena que contiene a todo elemento de Im f. Llamemos, pues, n = lm f.
Читать дальше

 X. Por el Axioma de amalgamación, Y es un conjunto. Cada elemento u de X es un conjunto y, por el Corolario3.3, u está bien ordenado. Elijamos su primer elemento. Definimos una aplicación
X. Por el Axioma de amalgamación, Y es un conjunto. Cada elemento u de X es un conjunto y, por el Corolario3.3, u está bien ordenado. Elijamos su primer elemento. Definimos una aplicación 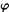 de manera que (u) sea el primer elemento de u , entonces
de manera que (u) sea el primer elemento de u , entonces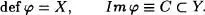
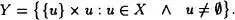
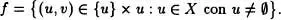
 k arbitrarios se verifica x ⊂ y ó y ⊂ x. Este concepto de cadena también se extiende para toda relación de orden arbitraria .
k arbitrarios se verifica x ⊂ y ó y ⊂ x. Este concepto de cadena también se extiende para toda relación de orden arbitraria .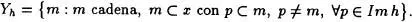
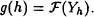
 . lamemos n este ordinal. Con ello se obtiene que, puesto que def f
. lamemos n este ordinal. Con ello se obtiene que, puesto que def f  def f, n
def f, n  , es decir, g(f) = g(f|deî ) = . Pero esto contradice el hecho de que g(f) es un elemento de Y), o lo que es lo mismo g(f) no sería una cadena. Por consiguiente, no hay ninguna cadena contenida en x y que contenga propiamente a cada elemento de Imf. Ahora bien, por construcción de /, Im f es una cadena, y cada miembro de Im f es una cadena por ser imagen de un ordinal. Entonces, en virtud del Lema 3.7,
, es decir, g(f) = g(f|deî ) = . Pero esto contradice el hecho de que g(f) es un elemento de Y), o lo que es lo mismo g(f) no sería una cadena. Por consiguiente, no hay ninguna cadena contenida en x y que contenga propiamente a cada elemento de Imf. Ahora bien, por construcción de /, Im f es una cadena, y cada miembro de Im f es una cadena por ser imagen de un ordinal. Entonces, en virtud del Lema 3.7, 










