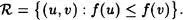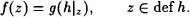
Consideremos ahora x 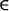
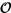 ~ def f . En virtud del Teorema 2.9 del Capítulo 1, f(x) = .
~ def f . En virtud del Teorema 2.9 del Capítulo 1, f(x) = .
Por otra parte, al ser def f conjunto, el Corolario 6.3 del capítulo citado asegura que / es conjunto.
En el caso de que f 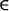 def g, el Teorema 2.9 citado afirma que g(f) es conjunto. Tomemos a continuación el ¿-primer elemento y de ~ def f y h = f
def g, el Teorema 2.9 citado afirma que g(f) es conjunto. Tomemos a continuación el ¿-primer elemento y de ~ def f y h = f 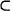 {y, g(f)}. Puesto que def h = def f
{y, g(f)}. Puesto que def h = def f 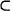 y también es saturado y es conectado por E. Luego def h es ordinal. A su vez se cumple de la misma definición de h que h(z) = g{h|z ) para todo z
y también es saturado y es conectado por E. Luego def h es ordinal. A su vez se cumple de la misma definición de h que h(z) = g{h|z ) para todo z 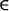 def h. Aplicando el Lema2.25, h ⊂ f . Esto conduce a que esta última aplicación h es de las que define la función f, lo que conduce a que y
def h. Aplicando el Lema2.25, h ⊂ f . Esto conduce a que esta última aplicación h es de las que define la función f, lo que conduce a que y 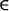 def f, que es contradictorio, ya que y
def f, que es contradictorio, ya que y 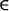
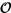 ~ def f.
~ def f.
Luego f  def g , entonces por las razones ya expuestas g(f) =
def g , entonces por las razones ya expuestas g(f) = 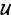 , con lo que
, con lo que
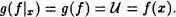
Con ello se ha probado que la relación anterior es válida para todo ordinal.
2.3 Axioma de elección. Proposiciones equivalentes
Definición 3.1: Una función de elección es una aplicación F de manera que F(x) x para cada elemento x no vacío del dominio de F.
Con este nuevo concepto, enunciamos el Axioma de elecciónen la modalidad dada por Godei :
VIII Axioma de elección
Existe un función de elección F cuyo dominio es ~ .
En realidad la función de elección selecciona un elemento de cada conjunto no vacío.
Si se restringe este axioma a cada conjunto no vacío se tiene la versión de este axioma dada por Zermelo :
Axioma de elección de Zermelo
Para cada conjunto no vacío X existe una función de elección
definida en P(X)~ (P(X): partes de X ).
Evidentemente el Axioma de elecciónimplica el Axioma de Zermelo.
Estudiemos sus consecuencias :
Los teoremas que vamos a probar se basan en el Axioma de elección;pero con pequeñas variantes en las demostraciones también son válidos a partir del Axioma de Zermelo.
.
Teorema 3.2: (de numerabilidad) Si x es un conjunto, existe una aplicación biyectiva, cuya imagen es x y su dominio es un número ordinal .
Demostración :
Construimos una función f de la siguiente manera: Sea la aplicación definida como g(h) = F{x ~ Im h ), donde h es conjunto. En virtud del Teorema2.26, existe una aplicación F , cuyo dominio es un ordinal y que verifica f(u) = g(f| u)para cada número ordinal u. Entonces f{u) = F{x~Im f|u).
Si u 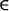 def f, f(u) es conjunto (Teorema 5.9 del Capítulo1), y por tanto
def f, f(u) es conjunto (Teorema 5.9 del Capítulo1), y por tanto

Probemos que f es una biyección: Partimos de

Si v, u son distintos, uno será mayor que el otro (por ser ordinales). Sea, por ejemplo, v < u. Y ello conduce a que f{v) Im f|u. Pero por (3.2.2), f(u) Im f| , que contradice (3.2.1). Luego / es una inyección.
Evidentemente def f ≠ 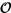 , pues de lo contrario f -1sería una aplicación, cuyo dominio sería una subclase de x y, por tanto, subconjunto (por serlo x). Por el Axioma de sustitución, Ö sería un conjunto, hecho que hemos probado que no lo es. Entonces def f £ . Llamemos u a def f.
, pues de lo contrario f -1sería una aplicación, cuyo dominio sería una subclase de x y, por tanto, subconjunto (por serlo x). Por el Axioma de sustitución, Ö sería un conjunto, hecho que hemos probado que no lo es. Entonces def f £ . Llamemos u a def f.
Puesto que def f  def f en virtud de la Proposición2.2, es decir, u no es elemento de def f, u deff/, y el Teorema 5.9 citado asegura que f(u) = y, por tanto, F(x ~ Im f) = . Pero el dominio de F es
def f en virtud de la Proposición2.2, es decir, u no es elemento de def f, u deff/, y el Teorema 5.9 citado asegura que f(u) = y, por tanto, F(x ~ Im f) = . Pero el dominio de F es 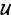 ~
~  , y aplicando de nuevo el Teorema 5.9,
, y aplicando de nuevo el Teorema 5.9,

es decir, x = Im f. Entonces f| defes una aplicación biyectiva entre el ordinal def f y el conjunto x.
El siguiente teorema también es debido a Zermelo :
Teorema 3.3:(de la buena ordenación) Todo conjunto admite un buen orden.
Demostración :
Consideremos un conjunto X. Por el teorema anterior, existe una biyección f entre X y un ordinal y. Construyamos a partir de f un buen orden en X , definiendo la relación de orden
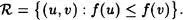
A su vez de este resultado deducimos la siguiente proposición :
Читать дальше

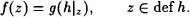
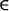
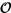 ~ def f . En virtud del Teorema 2.9 del Capítulo 1, f(x) = .
~ def f . En virtud del Teorema 2.9 del Capítulo 1, f(x) = . {y, g(f)}. Puesto que def h = def f
{y, g(f)}. Puesto que def h = def f  def g , entonces por las razones ya expuestas g(f) =
def g , entonces por las razones ya expuestas g(f) =  , con lo que
, con lo que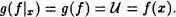


 , y aplicando de nuevo el Teorema 5.9,
, y aplicando de nuevo el Teorema 5.9,