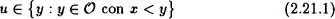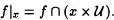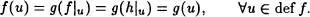Proposición 2.21: Si x 
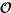 , entonces x + 1es ordinal y es el E-primer elemento de
, entonces x + 1es ordinal y es el E-primer elemento de
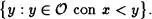
Demostración :
Evidentemente x  {x} es saturado, ya que x es un ordinal. Además E conecta a x
{x} es saturado, ya que x es un ordinal. Además E conecta a x  {x}, ya que x
{x}, ya que x  x
x  {x} y E conecta a x. Esto hace que x + 1 sea ordinal.
{x} y E conecta a x. Esto hace que x + 1 sea ordinal.
Supongamos que exista un elemento
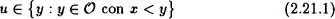
con u < x + 1 . Esto hace que u  x
x  {x}, con lo que, o u
{x}, con lo que, o u  x, o u = x. Pero por (2.21.1) x
x, o u = x. Pero por (2.21.1) x  u. Estas conclusiones contradicen las Proposiciones 2.1, 2.2, lo que prueba que x + 1 es el E -primer elemento de {y : y
u. Estas conclusiones contradicen las Proposiciones 2.1, 2.2, lo que prueba que x + 1 es el E -primer elemento de {y : y  O con x < y}.
O con x < y}.
Proposición 2.22: Si x 
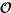 , se tiene que
, se tiene que  (x + 1) = x.
(x + 1) = x.
Trivial.
Definición 2.23: 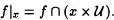
Proposición 2.24: Si f es una aplicación, f|x es una función de dominio def| x= x ⋂def f, y además

También es una proposición inmediata de la Definición 2.23.
Finalizamos esta Sección estudiando ei teorema final de los ordinales que, a su vez, precisa de un lema previo.
Lema 2.25: Sea f una aplicación tal que su dominio sea un ordinal y sea g una función que verifique f(u) = g(f|u) para cada u  def f. Si h es también una función de manera que su dominio sea un ordinal y h(u) = g(h|u) con u
def f. Si h es también una función de manera que su dominio sea un ordinal y h(u) = g(h|u) con u  def h, entonces h ⊂ f ó f ⊂ h. Demostración :
def h, entonces h ⊂ f ó f ⊂ h. Demostración :
Al ser def f y def h ordinales, podemos suponer que def f ⊂ def h (en virtud del Teorema 2.10).
Probemos que f(u) = h(u), ∀u  def f :
def f :
Supongamos que no se verifica. Consideremos que u sea el E-primer elemento de def f tal que F(u) ≠ h(u). Entonces f(v) = h(v) para los elementos v E-anteriores a u , es decir, v  u. Esto hace que f|u = h| u. En consecuencia,
u. Esto hace que f|u = h| u. En consecuencia,
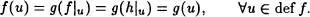
Sabido esto, como las imágenes de estas dos funciones coinciden en def f, resulta que f ⊂ h.
Se prueba la inclusión contraria si se hubiera partido de def h ⊂ def f .
Teorema 2.26: Para cada g existe una función f, cuyo dominio def / es un ordinal, que verifica f(x) = g(f|x) para todo número ordinal x.
Demostración :
Probaremos este teorema tanto para ordinales x  def f como para los que x def f.
def f como para los que x def f.
Para el primer caso, definamos la relación binaria f del siguiente modo: Los pares ordenados (u, v)  f verifican u s
f verifican u s  . Para definir la segunda componente, tomemos una aplicación h cuyo dominio def h sea un ordinal y que verifique que h(z) = g(h|z) para cada z
. Para definir la segunda componente, tomemos una aplicación h cuyo dominio def h sea un ordinal y que verifique que h(z) = g(h|z) para cada z  def h. (Sobre la existencia de h , hemos de decir que se construye a partir de un ordinal z, pues de este modo queda definida para los ordinales y
def h. (Sobre la existencia de h , hemos de decir que se construye a partir de un ordinal z, pues de este modo queda definida para los ordinales y  z). Entonces elegimos v de manera que (u, v)
z). Entonces elegimos v de manera que (u, v)  h.
h.
Debido a que las restricciones de h coinciden (Lema2.25), f es una función. Además, de la definición de sección (Definición1.5) y de la Proposición2.8, resulta que def f es una E-sección de 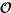 y, por tanto, es un ordinal (Teorema2.15). Es más: Dado que h(z) = g(h|z ) para z
y, por tanto, es un ordinal (Teorema2.15). Es más: Dado que h(z) = g(h|z ) para z  def h , por definición de f , h ⊂ f , con lo que
def h , por definición de f , h ⊂ f , con lo que
Читать дальше


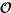 , entonces x + 1es ordinal y es el E-primer elemento de
, entonces x + 1es ordinal y es el E-primer elemento de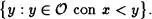
 {x} es saturado, ya que x es un ordinal. Además E conecta a x
{x} es saturado, ya que x es un ordinal. Además E conecta a x