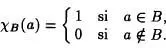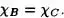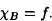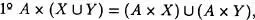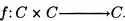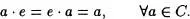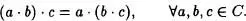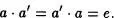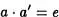Demostración :
1 ºTomemos f 
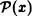 , luego f C x × y es conjunto. Esto hace que
, luego f C x × y es conjunto. Esto hace que 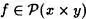 , es decir que
, es decir que
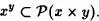
Pero el Teorema2.7 asegura que 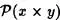 es un conjunto, puesto que x × y lo es. Entonces apliquemos el Teorema2.1, y con ello afirmamos que xy es un conjunto.
es un conjunto, puesto que x × y lo es. Entonces apliquemos el Teorema2.1, y con ello afirmamos que xy es un conjunto.
2 ºSea B un subconjunto arbitrario de A (B  A). Por función característica de B se entiende una aplicación
A). Por función característica de B se entiende una aplicación 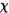 B: A →{0,1} definida por
B: A →{0,1} definida por
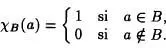
Con esta clase de funciones, definimos la aplicación

Veamos que es biyectiva :
Estudiemos en primer lugar la inyectividad de 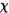 Supo
Supo 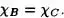
Esto hace que si b  B se tiene que
B se tiene que 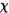 c (b)=
c (b)= 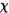 B (b)= 1, de donde b
B (b)= 1, de donde b  C.
C.
Esto prueba que B  C.
C.
La inclusión contraria se prueba de la misma manera.
Veamos la suprayectividad: Tomemos f : A → {0,1}, y definimos B = f-1( 1). Evidentemente
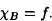
En lo sucesivo, representaremos el conjunto de partes de un conjunto x indistintamente por 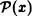 o por 2X.
o por 2X.
Proposición 6.7:
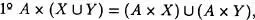
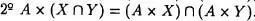
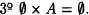
Demostración :
Simple aplicación del Axioma de extensióny de las definiciones implicadas.
En cuanto a las leyes de composición diremos que hay de dos tipos: internas y externas. Estas últimas también pueden ser reconocidas por acciones o transformaciones , si poseen propiedades específicas. Estudiemos en primer lugar las primeras :
Definición 6.8:Una ley de composición interna definida en un conjunto C es una aplicación
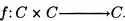
Es costumbre representar estas leyes por los símbolos -, •, + , etc. Así por ejemplo f(a,b ) = a • b , o f(a,b) = a * b, o f(a,b) = a • b , o f(a,b) = a + b.
Enunciamos a continuación a título de definiciones las propiedades más usuales que pueden tener estas leyes :
Definición 6.9:Se dice que una ley de composición interna posee elemento neutro o elemento unidad e  C si
C si
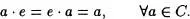
Si sólo se verifica

se dirá que e es elemento neutro por la derecha; y si se cumple que

será el elemento neutro por la izquierda.
Definición 6.10: Una ley de composición interna se dice que g.oza de la propiedad asociativa si
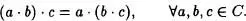
Definición 6.11:Sea una ley de composición interna con elemento unidad e, definida en un conjunto C. Se dice que un elemento a  C posee elemento simétrico a' si
C posee elemento simétrico a' si
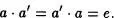
En el caso de que se verifique sólo
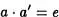
se dirá que a' es elemento simétrico de a por la derecha. Del mismo modo se define elemento simétrico por la izquierda.
Definición 6.12:Una ley de composición interna definida en un conjunto C verifica de la propiedad conmutativa si

Definición 6.13: Dadas dos leyes de composición internas • definidas en un mismo conjunto C, se dice que la ley • posee la propiedad distributiva respecto a la ley * si para todo a,b,c G C se verifica
Читать дальше


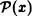 , luego f C x × y es conjunto. Esto hace que
, luego f C x × y es conjunto. Esto hace que 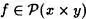 , es decir que
, es decir que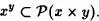
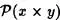 es un conjunto, puesto que x × y lo es. Entonces apliquemos el Teorema2.1, y con ello afirmamos que xy es un conjunto.
es un conjunto, puesto que x × y lo es. Entonces apliquemos el Teorema2.1, y con ello afirmamos que xy es un conjunto. A). Por función característica de B se entiende una aplicación
A). Por función característica de B se entiende una aplicación 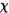 B: A →{0,1} definida por
B: A →{0,1} definida por