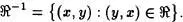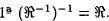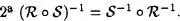1 ...7 8 9 11 12 13 ...23 Definición 3.10: Sea z una clase. Llamaremos primera componente de z a z; y segunda componente de z a ( z ) (( z) ~ z )
Teorema 3.11:
1º Si x e y son conjuntos, la primera componente del par (x, y) es x; y la segunda componente es y.
2ºSi x ó y no es conjunto, la primera y la segunda componentes de (x, y) son U.
Demostración :
1 ºLa primera componente de (x,y) se obtiene directamente de la
Proposición 3.9,4º.
En cuanto a la segunda, calculemos

Pero
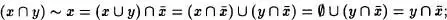
y sustituyendo

Si x ó y no es un conjunto, hemos visto que 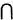
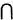 =
=  , decir que la primera componente del par es
, decir que la primera componente del par es  .
.
Calculemos la segunda componente :
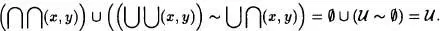
Corolario 3.12: Si x e y son conjuntos y (x,y) = (u, v), entonces x = u, y = v.
Demostración :
En virtud de la Proposición 3.8, ( x,y ) es un conjunto, y por tanto (w, v) también es conjunto. Y la misma proposición conduce a que u y v son conjuntos. El resto de la demostración es aplicación trivial del Teorema 3.11.
1.4 Relaciones binarias
Iniciamos el estudio de las relaciones binarias. En pocas palabras consisten en algumos tipos de clases de pares ordenados. Daremos en esta Sección sus propiedades generales. A continuación nos dedicaremos a desarrollar las relaciones binarias más importantes como son el concepto de función o aplicación, y el de relación binaria de equivalencia.
Definición 4.1: Una clase se dice que es una relación binaria si para cada elemento z 
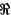 existen x e y tales que z = (x,y).
existen x e y tales que z = (x,y).
El concepto composición de relaciones binarias viene dado por :
Definición 4.2:Sean R y S relaciones binarias. Llamaremos R o S a la clase
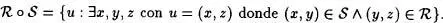
Si una relación binaria permite ser compuesta consigo misma de nanera que = o , se dice que posee la Propiedad transitiva.
De esta última definición se deduce directamente :
Corolario 4.3:.
Proposición 4.4:
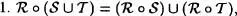
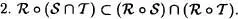
Demostración :
Probemos la segunda. Sea (x,z) 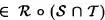 . Existe un y de manera que
. Existe un y de manera que 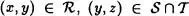 . En consecuencia, (y, z)
. En consecuencia, (y, z)  S, ( y,z )
S, ( y,z )  T. Es decir que (x,z)
T. Es decir que (x,z)  R o S y ( x, z )
R o S y ( x, z )  R o T. Esto hace que
R o T. Esto hace que 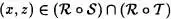 .
.
Para la primera expresión, se procede del mismo modo.
Definición 4.5:Sea 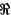 un una relación binaria. Se define la relación inversa
un una relación binaria. Se define la relación inversa 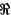 -1de
-1de 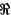 como
como
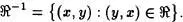
Si una relación binaria cumple que = -1, se dirá que posee la
Propiedad simétrica.
Consecuencias inmediatas de esta última definición son
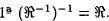
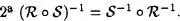
Para terminar esta Sección, enunciaremos algunas propiedades adicionales que pueden poseer las relaciones binarias :
Definición 4.6: Una relación binaria R se dice que está dotada de la Propiedad reflexiva, si dado (x,y) R, se cumple (x,x),(y,y) R .
Definición 4.7: Una relación binaria R posee la Propiedad antisimétrica si dados (x,y),(y,x) se tiene x = y .
Definición 4.8: Una relación binaria 1Z posee la Propiedad asimétrica cuando siempre que suceda que (x, y) R sea falso que (y, x) R .
1.5 Aplicaciones o funciones
Читать дальше


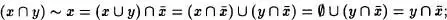

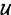 , decir que la primera componente del par es
, decir que la primera componente del par es 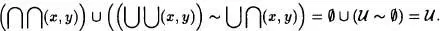

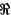 existen x e y tales que z = (x,y).
existen x e y tales que z = (x,y).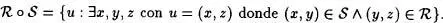
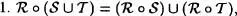
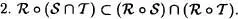
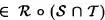 . Existe un y de manera que
. Existe un y de manera que 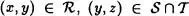 . En consecuencia, (y, z)
. En consecuencia, (y, z) 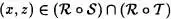 .
.