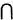Demostración :
En cuanto a la primera inclusión, tomemos un z arbitrario y analicemos la siguiente implicación

Al ser falsa 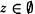 , resulta que esta implicación es verdadera, independientemente del valor de verdad que tenga z
, resulta que esta implicación es verdadera, independientemente del valor de verdad que tenga z  x.
x.
En la 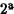 inclusión se razona del siguiente modo: Sea z
inclusión se razona del siguiente modo: Sea z  x. , entonces z es conjunto y , por tanto, z
x. , entonces z es conjunto y , por tanto, z 
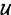 . En virtud de la Definición 1.14,
. En virtud de la Definición 1.14, 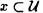
Obsérvese que de la definición de la clase vacía es falso que 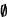

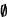 en cambio, sí tiene sentido
en cambio, sí tiene sentido 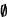

 , en virtud de este teorema.
, en virtud de este teorema.
Para finalizar esta Sección enunciaremos algunas propiedades más, de las que omitiremos sus demostraciones por considerarlas inmediatas si nos atenemos a las definiciones establecidas.
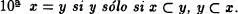
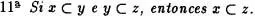
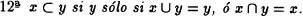

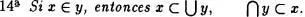
1.2 Subconjuntos
Los dos axiomas establecidos en la sección precedente resultan insuficientes para estudiar todas las propiedades de los conjuntos. Así por ejemplo, todavía no podemos saber si las subclases de un conjunto son conjuntos, o que la intersección de dos conjuntos es conjunto. Igualmente desconocemos qué sucede con la unión de dos conjuntos. Necesitamos, pues, de más axiomas. Uno de ellos se refiere a los llamados subconjuntos, que son subclas propias
III Axioma de subconjuntos
Si x es un conjunto ,existe un conjunto Y tal que para cada z

Teorena 2.1:Si x es un conjunto y z  x , entonces z es un conjunto.
x , entonces z es un conjunto.
Demostración :
Tomemos un z  x . Al ser x conjunto, podemos aplicar el axioma III, con lo que existe un conjunto Y tal que z
x . Al ser x conjunto, podemos aplicar el axioma III, con lo que existe un conjunto Y tal que z  Y. Esto hace que z sea un conjunto, en virtud de la Definición 1.2.
Y. Esto hace que z sea un conjunto, en virtud de la Definición 1.2.
Entonces se dirá que z es subconjunto de x.
Corolario 2.2: 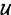 no es conjunto.
no es conjunto.
Demostración :
La clase de Russell R es subclase de 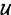 (falta por ver si coincide con
(falta por ver si coincide con 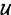 ). Entonces R . Si
). Entonces R . Si 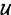 fuera conjunto, R sería conjunto. Y ello conduciría directamente a la paradoja de Russell. Luego
fuera conjunto, R sería conjunto. Y ello conduciría directamente a la paradoja de Russell. Luego 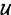 no es conjunto.
no es conjunto.
Corolario 2.3: Si una de las clases x, y es un conjunto, x y es un conjunto.
Demostración :
Supongamos que x sea un conjunto. De la Definición 1.3, 2- y la Definición 1.14, tenemos que x y x. Entonces el Teorema2.1 asegura que x y es un conjunto.
Teorema 2.4: 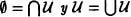 .
.
Demostración :
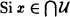 , resulta que x es un conjunto, y dado que
, resulta que x es un conjunto, y dado que 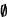
 x (Teorema 1.15),
x (Teorema 1.15), 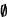 sería un conjunto. Ahora bien, de la Definición 1.12,
sería un conjunto. Ahora bien, de la Definición 1.12, 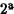 , todo elemento de
, todo elemento de 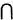
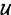 es elemento de
es elemento de 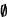 pero según vimos en el Teorema1.10,
pero según vimos en el Teorema1.10, 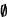 no tiene elementos, de lo que resulta que
no tiene elementos, de lo que resulta que 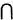
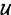 tampoco posee elementos. Por el Axioma de extensión,
tampoco posee elementos. Por el Axioma de extensión, 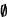 y
y 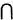
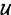 son iguales.
son iguales.
Читать дальше


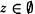 , resulta que esta implicación es verdadera, independientemente del valor de verdad que tenga z
, resulta que esta implicación es verdadera, independientemente del valor de verdad que tenga z  x.
x.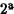 inclusión se razona del siguiente modo: Sea z
inclusión se razona del siguiente modo: Sea z 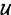 . En virtud de la Definición 1.14,
. En virtud de la Definición 1.14, 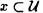
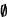

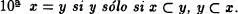
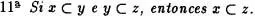
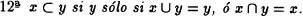

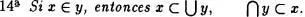

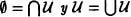 .
.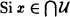 , resulta que x es un conjunto, y dado que
, resulta que x es un conjunto, y dado que