Respecto a los cuantores, haremos uso del cuantificador universal V (para todo) y del cuantificador existencial 3 (existe un).
Otras constantes que se emplean en matemáticas, como es G y otras que iremos utilizando a lo largo del texto.
El plan de nuestra exposición es introducir paulatinamente los axiomas a medida que se necesiten, con el fin de llegar a una teoría conjuntista si no completa (que no lo es, y tampoco podría serlo 1 ), al menos carente de contradicciones lógicas en el momento actual.
En primer lugar partimos de dos axiomas básicos :
I Axioma de extensión
Dos clases son iguales si los elementos de la primera pertenecen a la segunda; y los elementos de la segunda también son miembros de la primera clase. Dos clases x, y son iguales, se representará por
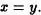
Un segundo axioma que necesitamos es
II Axioma de clasificación
La sentencia
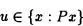
es equivalente afirmar que
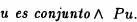
En realidad el Axioma de clasificaciónnos dice que la variable Xsometida a propiedades específicas, sentencias definitorias o fórmulas clasificatorias (simbolizadas por una función proposicional Px) puede ser sustituida por el conjunto u, Pu , es decir que u goza de las mismas propiedades que la variable x (además de ser conjunto).
Definición 1.3: Sean x, y clases,
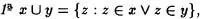
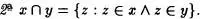
En la primera definición se lee “ x unión y ” y el símbolo U es conocido por unión.En la segunda se entiende “ x intersección y” y el símbolo fl es llamado intersección.
Las propiedades que se desprenden de estas definiciones se deducen inmediatamente del Axioma de clasificación :
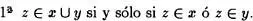
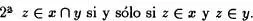
Las siguientes propiedades se prueban a partir del Axioma de extensióncon la ayuda de las Propiedades 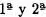
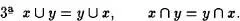
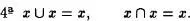
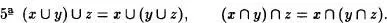
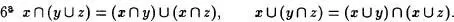
Definición 1.4: 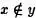 si y sólo si es falso
si y sólo si es falso 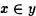
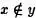 se lee “x no pertenece a y” .
se lee “x no pertenece a y” .
Definición 1.5:Sea x una clase. La clase complementaria 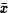 se define como
se define como
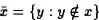
Proposición 1.6: = x.
Demostración :
Tomemos 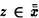 Luego es falso que
Luego es falso que 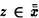 . Por la Definición 1.4,
. Por la Definición 1.4, 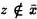 Y por la Definición 1.5,
Y por la Definición 1.5, 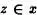 Con ello hemos probado que los elementos de la clase
Con ello hemos probado que los elementos de la clase 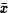 pertenecen a la clase x.
pertenecen a la clase x.
Invirtiendo el orden de la demostración, se prueba que los elementos de la clase x también pertenecen a la clase 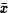
En virtud del Axioma de extensión, las dos clases son iguales.
Teorema (De Morgan):  .
.
Demostración :
Sólo probaremos una de ellas, por ejemplo la 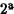 . Tomemos
. Tomemos 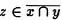 , luego es falso que
, luego es falso que 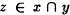 , es decir que
, es decir que 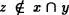 . En virtud de la Definición 1.3, Luego .
. En virtud de la Definición 1.3, Luego .
La inclusión contraria se obtiene invirtiendo el orden de la demostración.
De nuevo aplicamos el Axioma de extensiónpara afirmar que las dos clases son iguales.
Definición 1.7:Por complementario de y relativo a x, entenderemos
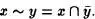
Con frecuencia se simboliza x ~ y por Cxy.
Proposición 1.8: 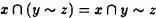 .
.
Читать дальше

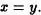
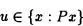
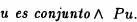
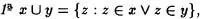
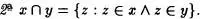
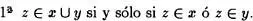
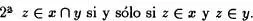
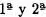
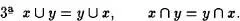
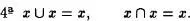
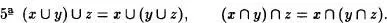
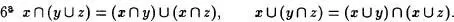
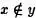 si y sólo si es falso
si y sólo si es falso 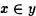
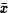 se define como
se define como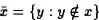
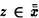 Luego es falso que
Luego es falso que 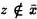 Y por la Definición 1.5,
Y por la Definición 1.5, 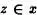 Con ello hemos probado que los elementos de la clase
Con ello hemos probado que los elementos de la clase  .
.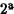 . Tomemos
. Tomemos 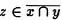 , luego es falso que
, luego es falso que 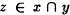 , es decir que
, es decir que 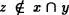 . En virtud de la Definición 1.3, Luego .
. En virtud de la Definición 1.3, Luego .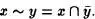
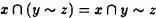 .
.










