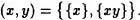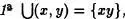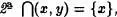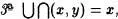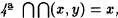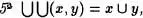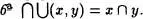Joaquín Olivert Pellicer - Estructuras de álgebra multilineal
Здесь есть возможность читать онлайн «Joaquín Olivert Pellicer - Estructuras de álgebra multilineal» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на испанском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Estructuras de álgebra multilineal
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Estructuras de álgebra multilineal: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Estructuras de álgebra multilineal»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.

 es un conjunto. Finalmente recurrimos al Teorema2.1, que conduce a que {x} es un conjunto.
es un conjunto. Finalmente recurrimos al Teorema2.1, que conduce a que {x} es un conjunto. U y que z = x , ya que por el Axioma de clasificación z es conjunto. Entonces es verdadera la implicación x => z = x para todo z .
U y que z = x , ya que por el Axioma de clasificación z es conjunto. Entonces es verdadera la implicación x => z = x para todo z .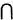 {x} = x y
{x} = x y 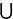 {x} = x ; si x no es un conjunto
{x} = x ; si x no es un conjunto 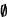 y
y 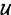 .
.
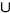 {y}. Esta clase se dice que es un par no ordenado.
{y}. Esta clase se dice que es un par no ordenado. y,
y,