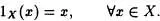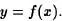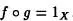1 ...8 9 10 12 13 14 ...23 En algunos tratados de álgebra se hace distinción entre aplicación y función. Hemos preferido no incorporarla en este libro, puesto que en todo este contexto no precisamos emplearla.
Definición 5.1: Una relación binaria f se dice función o aplicación si dados (x, y), (x, z) f se cumple y = z .
Definición 5.2: Se llama dominio de una aplicación f a
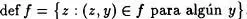
Rango o imagen de f se define como
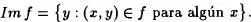
Una aplicación f se dice que es inyectiva si la relación binaria inversa f-1 es aplicación, es decir,

De las Definiciones 4.2 y 5.1se desprende trivialmente que
Proposición 5.3: Sean f, g funciones. Entonces f o g es función.
Notación 5.4: En lo sucesivo representaremos (x, y)  f por
f por
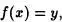
que es el modo habitual de representar las funciones. Además, si X es un conjunto, se define el “ conjunto imagen de X por la aplicación f” como
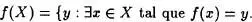
La notación inicial, como pares ordenados, se llamará gráfica de la aplicación , y será representada por el símbolo 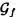 si la aplicación en cuestión es /.
si la aplicación en cuestión es /.
También se define
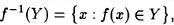
Los elementos de f-1(Y) son llamados “ antiimágenes de Y por la aplicación f” mientras que los elementos de f(X) se conocen con el nombre de “imágenes de X por f”.
Proposición 5.5: Sean f y g dos funciones. Entonces f = g si y sólo si f(x) = g(x) , ∀ x .
Demostración :
Llamemos y = f(x) = g(x). Debido a
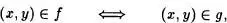
f = g en virtud del Axioma de extensión.
Vamos a introducir el quinto axioma :
V Axioma de sustitución
Si f es una función y su dominio def f es conjunto, entonces Imf es conjunto.
Proposición 5.6: Sean A, B dos aplicaciones. Entonces
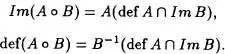
Demostración :
Tomemos un z  Im(AoB). Existe un x de manera que AoB(x) = z. Llamemos y = B(x) y por tanto z = A(y). Entonces y
Im(AoB). Existe un x de manera que AoB(x) = z. Llamemos y = B(x) y por tanto z = A(y). Entonces y  Im B, y def A, es decir,
Im B, y def A, es decir,
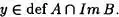
En consecuencia,
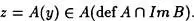
La inclusión contraria prueba invirtiendo el proceso de la demostración.
Probemos la última expresión. Elijamos un x  def(A o B) y llamemos y = B(x). Entonces y
def(A o B) y llamemos y = B(x). Entonces y  Im B con y
Im B con y  def A , es decir,
def A , es decir,
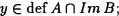
y por tanto,
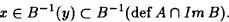
Veamos la inclusión contraria. Tomemos x  B-1(def A Im B). Esto hace que B(x)
B-1(def A Im B). Esto hace que B(x)  def A
def A  Im B , de donde B(x)
Im B , de donde B(x)  def A , y por tanto x def (A o B).
def A , y por tanto x def (A o B).
Definición 5.7:Una aplicación f que tome valores en X y sus imágenes estén en Y se escribe f : X → Y.
Una aplicación Ix : X → Xse dice que es la aplicación identidad sobre X
si
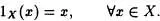
Una aplicación f : X → Yse dice que es suprayectiva, si para cada y  Y, existe un x
Y, existe un x  X tal que
X tal que
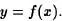
En virtud de la Proposición 5.5, la aplicación identidad es única.
Proposición 5.8:Consideremos f, g dos aplicaciones tales que
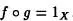
Entonces g es inyectiva y f suprayectiva. Demostración :
Читать дальше

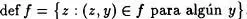
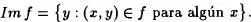

 f por
f por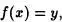
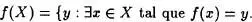
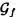 si la aplicación en cuestión es /.
si la aplicación en cuestión es /.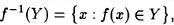
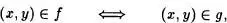
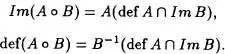
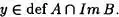
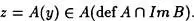
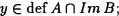
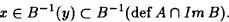
 Im B , de donde B(x)
Im B , de donde B(x)