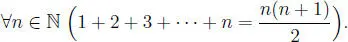(i) Si n ≥ n 0, entonces n + 1 ≥ n 0+ 1, luego n ∈ I 1y n ≥ n 0, entonces p ( n ) es verdad y, por la hipótesis del teorema, p ( n + 1) es verdad, por lo tanto, ( n + 1 ≥ n 0→ p ( n + 1)). Luego ( n + 1) ∈ I 1.
(ii) Si n 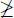 n 0se tiene n < n 0y, por lo tanto ( n + 1) ≤ n 0; luego:
n 0se tiene n < n 0y, por lo tanto ( n + 1) ≤ n 0; luego:
(a) Si ( n + 1) = n 0, entonces como p ( n 0) es verdad por hipótesis se tendrá que ( n + 1) ∈ I 1.
(b) Si ( n + 1) < n 0, entonces ( n + 1 ≥ n 0→ p ( n + 1) es verdad porque su antecedente es falso, por lo tanto, ( n + 1) ∈ I 1.
Hemos demostrado que I 1es un conjunto inductivo con lo que  ⊆ I 1, o sea ∀ n ∈
⊆ I 1, o sea ∀ n ∈  ( n ∈ I 1), o mejor ∀ n ∈
( n ∈ I 1), o mejor ∀ n ∈  ( n ≥ n 0) p ( n ).
( n ≥ n 0) p ( n ).
1.2.2 Segundo principio de inducción
El enunciado de este principio es el siguiente:
Sea p ( n ) una fórmula en n y n 0∈  , entonces:
, entonces:
(i)
[ p ( n 0) ∧ ∀ n ∈  [( n > n 0) ( p ( n 0) ∧ p ( n 0+ 1) ∧ · · · ∧ p ( n )) → p ( n + 1)]]
[( n > n 0) ( p ( n 0) ∧ p ( n 0+ 1) ∧ · · · ∧ p ( n )) → p ( n + 1)]]
↓
∀ n ∈  (( n > n 0) p ( n )).
(( n > n 0) p ( n )).
(ii)
[ p (1) ∧ ∀ n ∈  [( p (1) ∧ p (2) ∧ ··· ∧ p ( n )) → p ( n + 1)]] → ∀ n ∈
[( p (1) ∧ p (2) ∧ ··· ∧ p ( n )) → p ( n + 1)]] → ∀ n ∈  ( p ( n )).
( p ( n )).
Nota:
Es claro que (ii) es un caso particular de (i).
1.2.3 Otros conceptos
A causa de lo que estudiaremos con posterioridad, es necesario entregar algunas definiciones inductivas; éstas son:
Definición 1.2.1 Sea n ∈  se define la función factorial (!) del modo siguiente:
se define la función factorial (!) del modo siguiente:
1! = 1 ∧ ( n + 1)! = n !( n + 1).
Definición 1.2.2 Sea f :  →
→ 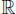 , se define la sumatoria desde k = 1 hasta k = n de los f ( k ) del modo siguiente:
, se define la sumatoria desde k = 1 hasta k = n de los f ( k ) del modo siguiente:
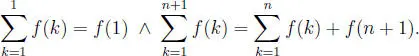
Definición 1.2.3 Sea f :  →
→ 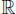 , se define la productoria desde k = 1 hasta k = n de los f ( k ) del modo siguiente:
, se define la productoria desde k = 1 hasta k = n de los f ( k ) del modo siguiente:
Definición 1.2.4 Sea p ∈  diremos que p es un número primo si:
diremos que p es un número primo si:
∀ n ∈  ∀ m ∈
∀ m ∈  ( p = n · m → ( n = 1 ∨ m = 1).
( p = n · m → ( n = 1 ∨ m = 1).
Definición 1.2.5 Sean p, q ∈  diremos que p y q son primos relativos si:
diremos que p y q son primos relativos si:
(∀ r ∈  )(∀ s ∈
)(∀ s ∈ 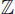 )(∀ t ∈
)(∀ t ∈ 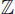 )[( p = r · s ∧ q = r · t ) → ( r = 1 ∨ r = −1)],
)[( p = r · s ∧ q = r · t ) → ( r = 1 ∨ r = −1)],
es decir, si el MCD ( p, q ) = 1
A continuación pasaremos a aplicar los principios de inducción resolviendo algunos problemas.
1.3 Problemas resueltos
Problema 1.3.1 Para el natural fijo n, calcular la suma:
S = 1 + 2 + 3 + ·· · + n.
Solución:
Se tiene:
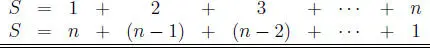
y sumando miembro a miembro estas dos igualdades, se obtiene:
2 S = ( n + 1) + ( n + 1) + ( n + 1) + ·· · + ( n + 1),
o sea:
2 S = n ( n + 1),
de donde:
S = 1 + 2 + 3 + ··· + n = 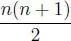 ,
,
que es el resultado pedido.
Nota:
En el problema siguiente, haremos ver que esta fórmula es válida para todo número natural.
Problema 1.3.2 Demostrar que:
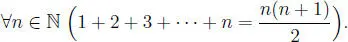
Solución:
Читать дальше

 n 0se tiene n < n 0y, por lo tanto ( n + 1) ≤ n 0; luego:
n 0se tiene n < n 0y, por lo tanto ( n + 1) ≤ n 0; luego: ⊆ I 1, o sea ∀ n ∈
⊆ I 1, o sea ∀ n ∈  , se define la sumatoria desde k = 1 hasta k = n de los f ( k ) del modo siguiente:
, se define la sumatoria desde k = 1 hasta k = n de los f ( k ) del modo siguiente: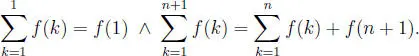
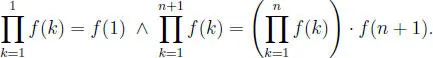
 diremos que p y q son primos relativos si:
diremos que p y q son primos relativos si: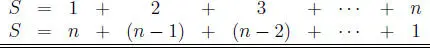
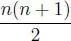 ,
,