Consideramos el conjunto:
haremos ver que este conjunto I es inductivo.
Que n = 1 ∈ I es evidente, pues:
Suponemos válido que n ∈ I , o sea:
Ahora deberemos probar que ( n + 1) ∈ I , es decir:
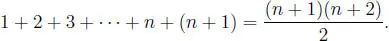
En efecto, se tiene:
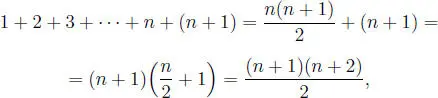
por lo tanto I es un conjunto inductivo. Esto quiere decir que:
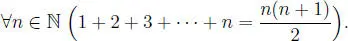
Problema 1.3.3 Para el natural fijo n, calcular la suma:
S = 1 2+ 2 2+ 3 2+ ··· + n 2.
Solución:
Se tiene:
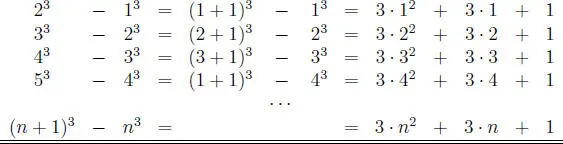
y sumando miembro a miembro estas dos igualdades, se obtiene:
( n + 1) 3− 1 = 3(1 2+ 2 2+ 3 2+ ··· + n 2) + 3(1 + 2 + 3 + ··· + n ) + n ,
o sea:
3(1 2+ 2 2+ 3 2+ ··· + n 2) = ( n + 1) 3− ( n + 1) − 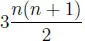 ,
,
de donde se consigue:
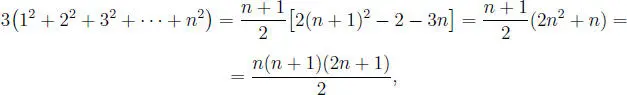
por consiguiente:
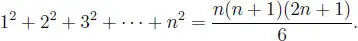
Notas:
(1) En el problema siguiente, haremos ver que esta fórmula es válida para todo número natural.
(2) En lo sucesivo, por comodidad, no escribiremos en las soluciones siguientes el conjunto I (que deberá establecerse que es inductivo); sólo probaremos para n = 1, aceptaremos para n y demostraremos para n + 1.
Problema 1.3.4 Demostrar que:
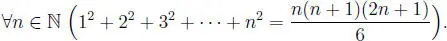
Solución:
Para n = 1 es evidente, pues:
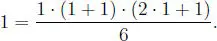
Suponemos el resultado válido hasta n, o sea:
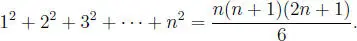
Ahora deberemos probarlo para ( n + 1), es decir:
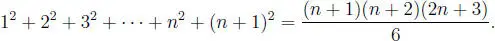
En efecto, se tiene:
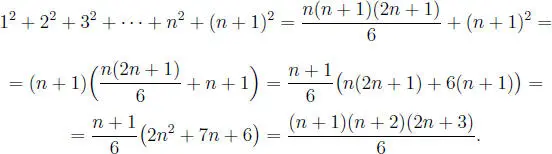
Problema 1.3.5 Para el natural fijo n, calcular la suma:
S = 1 3+ 2 3+ 3 3+ · ·· + n 3.
Solución:
Se tiene:
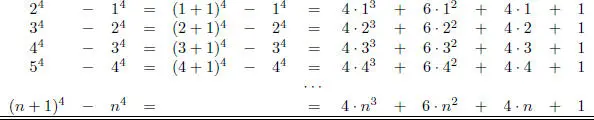
sumando miembro a miembro estas dos igualdades y factorizando adecuadamente, se obtiene:
1 3+ 2 3+ 3 3+ ··· + n 3= 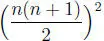 .
.
Nota:
En el problema siguiente, haremos ver que esta fórmula es válida para todo número natural.
Problema 1.3.6 Demostrar que:
∀ n ∈  [1 3+ 2 3+ 3 3+ ··· + n 3=
[1 3+ 2 3+ 3 3+ ··· + n 3= 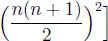 .
.
Solución:
A causa de la similitud con los problemas anteriores, la demostración queda a cargo del lector.
Problema 1.3.7 Demostrar que:
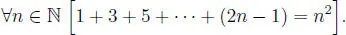
Solución:
Para n = 1 es evidente, pues:
1 = 1 2.
Suponemos el resultado válido hasta n, o sea:
1 + 3 + 5 + ··· + (2 n − 1) = n 2.
Ahora deberemos probarlo para ( n + 1), es decir:
1 + 3 + 5 + ··· + (2 n − 1) + (2 n + 1) = ( n + 1) 2.
En efecto, se tiene:
1 + 3 + 5 + ··· + (2 n − 1) + (2 n + 1) = n 2+ (2 n + 1) = n 2+ 2 n + 1 = ( n + 1) 2.
Problema 1.3.8 Demostrar que:
∀ n ∈ 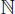 [(x − y) es divisor de ( xn − yn )].
[(x − y) es divisor de ( xn − yn )].
Solución:
Para n = 1 es evidente, puesto que x − y es factor de x − y . Suponemos ahora que x − y es divisor de xn − yn ; deberemos establecer que x − y es divisor de xn + 1− yn + 1.
Si a xn + 1− yn + 1le restamos y sumamos x yn , conseguiremos:
xn + 1− yn + 1= xn + 1− x yn + x yn − yn + 1= x( xn − yn ) + yn ( x − y ).
Como cada término de esta última expresión es divisible por x − y , también lo es xn + 1− yn + 1, lo que demuestra lo pedido.
Problema 1.3.9 Si a 1= a 2= 1 y an + 1 = 3 a n+ a n−1( n ≥ 2), entonces a ny a n + 1 son primos relativos .
Solución:
Vemos que a 1y a 2son primos relativos. Aceptemos la propiedad hasta n y supongamos que an y an + 1 noson primos relativos, o sea, existe el máximo común divisor entre an y a n−1y es MCD[ an , an + 1] = d ≠ 1, es decir, an + 1= pd y an = qd y como an + 1= 3 a n+ a n−1resulta pd = 3 qd + a n−1, luego a n−1= ( p − 3 q ) d , MCD[ an , a n−1]= d ≠ 1, lo que es una contradicción, puesto que
Читать дальше

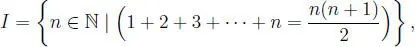
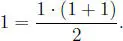
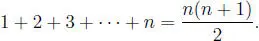
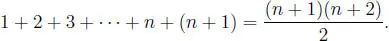
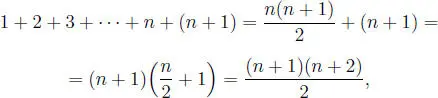
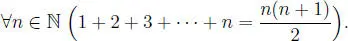
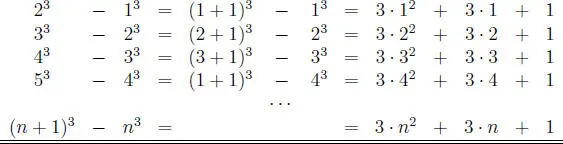
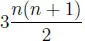 ,
,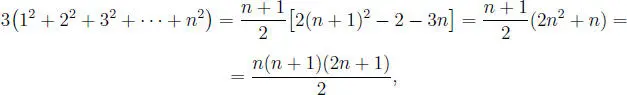
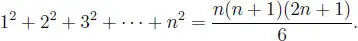
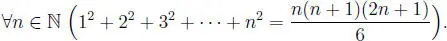
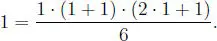
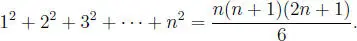
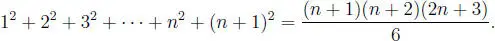
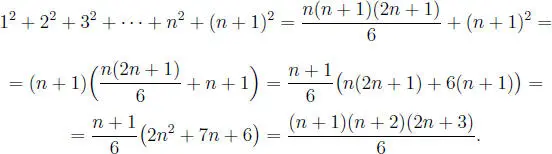
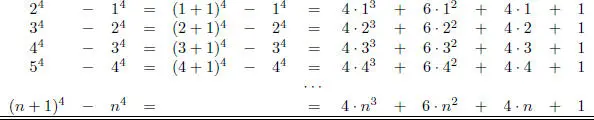
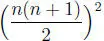 .
. [1 3+ 2 3+ 3 3+ ··· + n 3=
[1 3+ 2 3+ 3 3+ ··· + n 3= 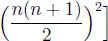 .
.