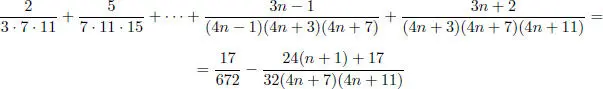
Demostración:
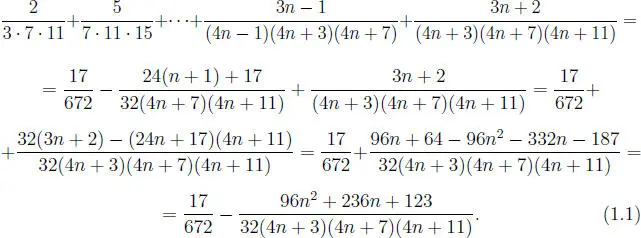
Pero:
(96 n 2+ 236 n + 123) : (4 n + 3) = 24 n + 41 = 24( n + 1) + 17,
o sea:
(96 n 2+ 236 n + 123) = (4 n + 3) · (24( n + 1) + 17). (1.2)
De (1.1) y (1.2) se sigue el resultado, es decir:
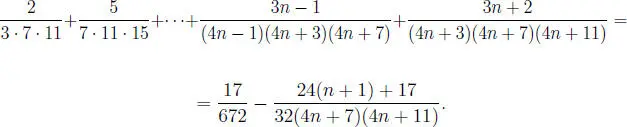
Problema 1.3.16 Sea f :  →
→ 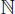 la función definida recursivamente por
la función definida recursivamente por
f (1) = 7, f (2) = 17, para n ≥ 3 ( f (n) = 5 f ( n − 1) − 6 f ( n − 2)),
demostrar que:
f ( n ) = 2 n + 1+ 3 n.
Solución:
Para resolver este problema utilizaremos el principio inductivo. Pues bien, tenemos que probar que f ( n ) = 2 n + 1+ 3 npara todo n ∈ 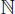 ; vemos que:
; vemos que:
f (1) = 2 1 + 1+ 3 1= 2 2+ 3 = 4 + 3 = 7
f (2) = 2 2 + 1+ 3 2= 2 3+ 3 2= 8 + 9 = 17
o sea, resultan los valores dados por medio de la definición recursiva. Suponemos entonces que:
f(n) = 2 n + 1+ 3 n
para los naturales 1, 2, 3, 4, ... , n .
Deberemos establecer ahora que:
f ( n + 1) = 2 n + 2+ 3 n + 1. (1.3)
En efecto, a causa de la definición recursiva tenemos que:
f ( n + 1) = 5 f ( n ) − 6 f ( n − 1) (1.4)
y como:
f ( n ) = 2 n + 1+ 3 n(1.5)
f ( n − 1) = 2 n + 3 n−1. (1.6)
De (1.4), (1.5) y (1.6) resulta:
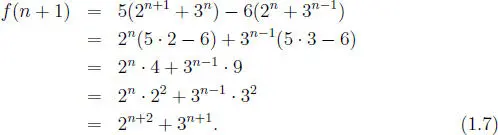
comparando (1.3) y (1.7) vemos que se obtiene lo pedido y por tanto:
∀ n ∈ 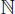 f ( n ) = 2 n + 1+ 3 n.
f ( n ) = 2 n + 1+ 3 n.
Problema 1.3.17 Sea f : 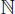 →
→ 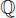 la función definida por:
la función definida por:
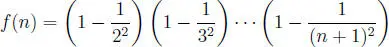
demostrar que f ( n ) = 
Solución:
Nuevamente utilizaremos el principio inductivo. Tenemos:
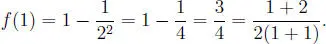
Suponemos la validez de la tesis del problema para 1, 2, 3, ... , n, o sea que:
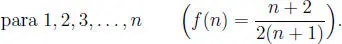
Deberemos probar que:

Procedamos, del enunciado tenemos que:
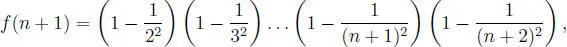
o sea:
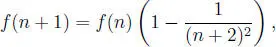
de donde:
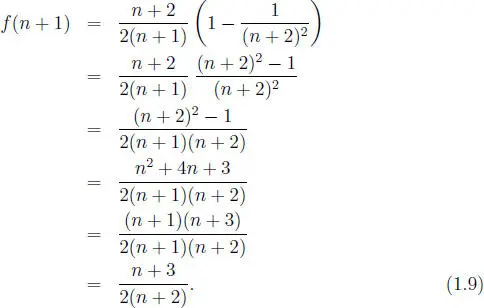
De (1.8) y (1.9) observamos que se obtiene lo pedido y por lo tanto:
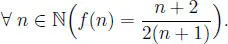
Problema 1.3.18 Sean a 1, a 2, ··· , an ∈ 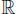 + , no todos iguales a 1 y tales que a 1· a 2· ·· an = 1, entonces:
+ , no todos iguales a 1 y tales que a 1· a 2· ·· an = 1, entonces:
∀ n ∈ 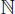 ( a 1+ a 2+ ··· + an > n ).
( a 1+ a 2+ ··· + an > n ).
Solución:
Ocuparemos el principio de inducción.
Sean a 1, a 2∈ 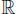 +, no ambos iguales a 1 y tales que a 1· a 2= 1. Como uno de ellos no es 1, no se pierde generalidad al suponer a 1≠ 1 y como a 2=
+, no ambos iguales a 1 y tales que a 1· a 2= 1. Como uno de ellos no es 1, no se pierde generalidad al suponer a 1≠ 1 y como a 2=  , se tiene tambien a 2≠ 1. Como ambos son positivos, uno de ellos es mayor que 1 y el otro menor que 1; puesto que si ambos fueren menores que 1, su producto sería menor que 1 (el argumento es similar, si ambos fueran mayores que 1). Supongamos entonces que a 1< 1 y a 2> 1, luego:
, se tiene tambien a 2≠ 1. Como ambos son positivos, uno de ellos es mayor que 1 y el otro menor que 1; puesto que si ambos fueren menores que 1, su producto sería menor que 1 (el argumento es similar, si ambos fueran mayores que 1). Supongamos entonces que a 1< 1 y a 2> 1, luego:
a 2− 1 > 0 y 1 − a 1> 0,
por lo tanto, se consigue:
( a 2− 1)(1 − a 1) > 0,
con lo que:
a 2+ a 1− 1 − a 1· a 2> 0, (1.10)
es decir:
a 1+ a 2> 1 + a 1· a 2= 2.
Supongamos ahora que la proposición es verdadera para cualquier colección de n números reales positivos.
Sean a 1, a 2, ··· , an , an + 1∈ 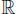 +, ( n + 1) números que cumplen con las hipótesis de la proposición, queremos demostrar que:
+, ( n + 1) números que cumplen con las hipótesis de la proposición, queremos demostrar que:
a 1+ a 2+ ··· + an + an + 1> n + 1 .
Como no todos ellos son iguales a 1 y el producto de todos ellos es 1, debe haber alguno mayor que 1 y otro menor que 1. Sin pérdida de generalidad, podemos suponer a 1< 1 y a 2> 1 y sea a = a 1· a 2.
Читать дальше

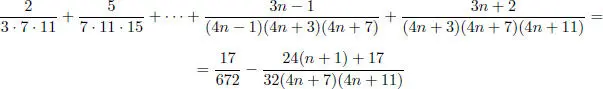
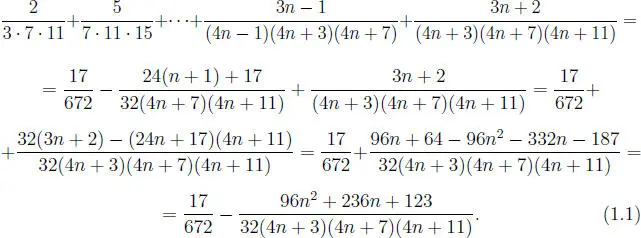
 →
→ 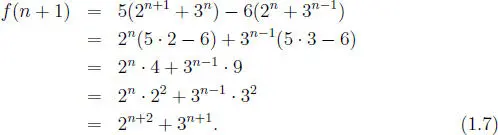
 la función definida por:
la función definida por: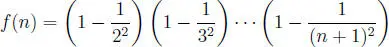

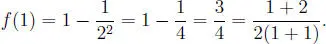
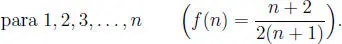

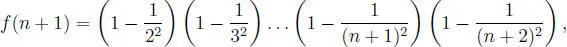
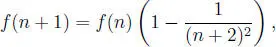
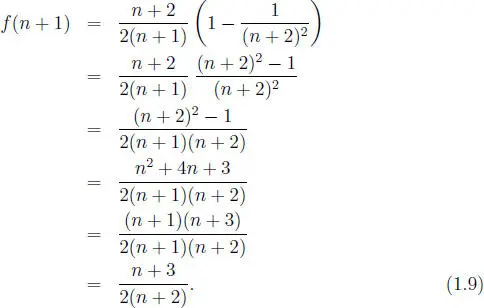
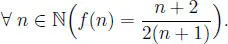
 + , no todos iguales a 1 y tales que a 1· a 2· ·· an = 1, entonces:
+ , no todos iguales a 1 y tales que a 1· a 2· ·· an = 1, entonces: , se tiene tambien a 2≠ 1. Como ambos son positivos, uno de ellos es mayor que 1 y el otro menor que 1; puesto que si ambos fueren menores que 1, su producto sería menor que 1 (el argumento es similar, si ambos fueran mayores que 1). Supongamos entonces que a 1< 1 y a 2> 1, luego:
, se tiene tambien a 2≠ 1. Como ambos son positivos, uno de ellos es mayor que 1 y el otro menor que 1; puesto que si ambos fueren menores que 1, su producto sería menor que 1 (el argumento es similar, si ambos fueran mayores que 1). Supongamos entonces que a 1< 1 y a 2> 1, luego:










