Mathias Blanz - Forschungsmethoden und Statistik für die Soziale Arbeit

Eine zusätzliche Qualitätsverbesserung bei fehlender Zufallsauswahl kann dadurch erzielt werden, dass für bestimmte Merkmale (wie z. B. Geschlecht oder Alter), die man für untersuchungsrelevant hält, Quoten festgelegt und diese bei der Ziehung berücksichtigt werden (sog. Quotenstichprobe). »Bei der Quotenstichprobe wird versucht, die Zusammensetzung der Stichprobe hinsichtlich ausgewählter Merkmale den Populationsverhältnissen durch bewusste Auswahl ›passender‹ Objekte anzugleichen, also quasi ›Quoten‹ für bestimmte Merkmale zu erfüllen« (Bortz & Döring, 2006, S. 402). Dazu ist es allerdings notwendig, dass Informationen über diese Quoten in der Population bekannt sind (z. B. aus amtlichen Statistiken). Ein Beispiel wäre: Da der Kindergarten X (Stichprobe) aufgrund seiner Lage überproportional viele Kinder mit Migrationshintergrund im bundesweiten Vergleich (Population) aufweist, wird von diesen Kindern nur ein Teil in die Studie aufgenommen.

Als weiteres nichtprobabilistisches Auswahlverfahren sei noch auf die sog. theoretische Stichprobe hingewiesen. Diese spielt insbesondere in der qualitativen Sozialforschung eine große Rolle und bezeichnet ein Vorgehen, bei dem die Forschenden auf der Grundlage theoretischer Vorüberlegungen typische und/oder untypische Fälle gezielt auswählen. Aufbauend auf dem Konzept der »exemplarischen Verallgemeinerung« (Wahl, Honig & Gravenhorst, 1982, S. 206) dienen dabei »detaillierte Einzelfallbeschreibungen, die ›repräsentativ‹ sind, wenn sie als typische Vertreter einer Klasse ähnlicher Fälle gelten können« (Bortz & Döring, 2006, S. 335), als Ausgangspunkt. Dies bedeutet auch, dass noch während der Datenerhebung neue (ähnliche oder kontrastierende) Fälle mit aufgenommen (oder ggf. ausgeschlossen) werden können. Eine Schwierigkeit dabei ist jedoch, dass unklar bleibt, wie Forschende einen typischen Fall erkennen können, ohne bereits über eine »Theorie« zu verfügen. Eine nachfolgende quantitative Untersuchung zur Überprüfung der Befunde solcher Studien erscheint deshalb notwendig.

Für zufallsbasierte Stichproben differenziert Tabelle 2 zwei Arten von Auswahlverfahren. Bei Zufallsstichproben wählt der Forschende nach dem Zufallsprinzip einzelne Merkmalsträger aus der Grundgesamtheit aus (z. B. werden im Rahmen einer »kleineren« empirischen Studie, in der alle Kinder des Kindergartens X als Population dienen, einzelne Kinder nach Zufall ausgewählt). Dies ist in Abbildung 4 in dem ersten Beispiel (ganz oben) dargestellt. Die Personen sind dabei ausschließlich in Hinblick auf das Populations-definierende Merkmal gleich (Kinder des Kindergartens X), weshalb dieses Vorgehen auch als einstufiges Auswahlverfahren bezeichnet wird. Die Zufallsauswahl kann dabei entweder ohne eine Systematik erfolgen (z. B. per Los; sog. einfache Zufallsstichprobe), bei der alle möglichen Kombinationen an MerkmalsträgerInnen entstehen können (z. B. die Kinder 2, 3, 5, 14 etc.), oder mit einer Systematik (z. B. jedes zweite Kind wird ausgewählt; sog. systematische Zufallsstichprobe), bei der nicht alle Kombinationen an MerkmalsträgerInnen auftreten können (z. B. die Kinder 2, 4, 6, 8 usw.). Bei der geschichteten Zufallsstichprobe (vgl. dazu das zweite Beispiel in Abbildung 4) wird zunächst die Grundgesamtheit nach einer Schichtungsvariablen (z. B. Geschlecht) unterteilt, und anschließend proportional zur jeweiligen Schicht eine Anzahl an Personen zufällig ausgewählt. Ein solches Vorgehen wird als zweistufiges Verfahren bezeichnet (erste Stufe: Schichtung, zweite Stufe: Zufallsauswahl). Befinden sich im Kindergarten X beispielsweise mehr Mädchen (zwei Drittel) als Jungen (ein Drittel), dann wird entweder per Los (ohne Systematik) oder per Position (mit Systematik) eine Stichprobe gezogen, die ebenfalls zwei Drittel Mädchen und ein Drittel Jungen beinhaltet.

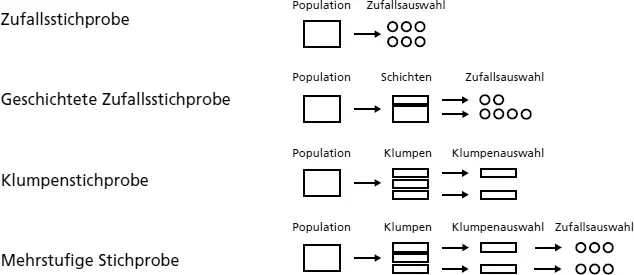
Abb. 4: Varianten zufallsbasierter (probabilistischer) Stichproben (nach Selg & Bauer, 1971)

Anstelle einer Schichtung können in einem zweistufigen Verfahren auch sog. Klumpen (oder Teilmengen) verwendet werden (vgl. drittes Beispiel in Abbildung 4). Im Unterschied zu Schichten (z. B. Geschlecht) stellen Klumpen »ein verkleinertes Abbild der Grundgesamtheit« (Ostermann & Wolf-Ostermann, 2012, S. 23) dar. Bezogen auf den Kindergarten X stellen beispielsweise die Bären-, die Krokodil- und die Hasengruppe drei Klumpen dar. Bei einer Klumpenstichprobe wird die Population zunächst in Teilmengen unterteilt (sog. Auswahleinheiten) und anschließend einige dieser Teilmengen nach dem Zufallsprinzip (ohne oder mit System) als ganze Gruppen zur Datenerhebung ausgewählt (z. B. die Bären- und die Hasengruppe; sog. Erhebungseinheiten). Eine gelungene Klumpenbildung setzt voraus, dass die MitgliederInnen eines Klumpens keine größere Ähnlichkeit zueinander aufweisen als die Merkmalsträger der Population. Wird diese Voraussetzung verletzt, führt dies zu einem vergrößerten Stichprobenfehler. Schließlich besteht noch die Möglichkeit, anstelle ganzer Klumpen eine Zufallsauswahl aus den jeweiligen Teilmengen zu ziehen. Dies stellt das letzte Beispiel zufallsbasierter (probabilistischer) Stichproben in Abbildung 4 dar (ganz unten) und wird als mehrstufige Stichprobe bezeichnet. Im Beispiel würde man dazu aus der Bären- und der Hasengruppe nach Zufall (ohne oder mit Systematik) einzelne Kinder für die Stichprobe auswählen.

Ein solches Vorgehen ist insbesondere dann ratsam, wenn die Grundgesamtheit über ein großes räumliches Gebiet verstreut ist. Dazu noch ein weiteres Beispiel: Es soll eine Befragung zu den Arbeitsbedingungen von Sozialpädagoginnen und Sozialpädagogen in kommunalen Beratungsstellen durchgeführt werden. Da es schwierig ist, alle SozialpädagogInnen in allen deutschen Beratungsstellen zu befragen, wird eine mehrstufige Stichprobe gebildet. Hierfür wird zunächst eine vollständige Liste mit allen Kommunen, die Beratungsstellen anbieten, erstellt. Danach wird eine zufällige Auswahl von den zu untersuchenden Kommunen getroffen. Im nächsten Schritt werden alle Arten von Beratungsstellen (z. B. für Ehe und Familie, Sucht, Senioren und Menschen mit Behinderungen, Schwangere usw.) der zu untersuchenden Kommunen aufgelistet und per Zufall jeweils eine davon ausgewählt. Im Anschluss wird eine zufällige Auswahl von SozialpädagogInnen aus den gezogenen Einrichtungen getroffen.

Abschließend sei noch auf Stichproben mit Messwiederholungen hingewiesen. So wird beispielsweise bei Längsschnittstudien dieselbe empirische Untersuchung (zumeist eine Befragung) zu mehreren Zeitpunkten durchgeführt und die Befunde der einzelnen Erhebungswellen miteinander verglichen. Während bei einer Panelstudie dieselben Personen mehrmals über einen Zeitraum erfasst werden (ein Beispiel ist das Sozio-oekonomische Panel, SOEP, bei dem jährlich über 12.000 Privathaushalte in Deutschland befragt werden), werden bei einer Trendstudie (auch: replikativer Survey) in jeder Erhebungswelle unterschiedliche Personen erfasst (ein Beispiel ist ALLBUS, die Allgemeine Bevölkerungsumfrage der Sozialwissenschaften, bei der i. d. R. alle zwei Jahre mehrere Tausend TeilnehmerInnen zu Einstellungen, Verhalten und Sozialstruktur interviewt werden) und in einer Kohortenstudie Personen bestimmter Altersklassen (Jahrgänge), wie zum Beispiel bei epidemiologischen und entwicklungspsychologischen Fragestellungen.

Die Stichprobengröße beeinflusst zusammen mit der Auswahlstrategie (zufallsbasiert versus nicht zufallsbasiert) und dem Forschungsdesign (explorativ, deskriptiv, explanativ) die Gültigkeit (Validität) einer sozialwissenschaftlichen Stichprobenuntersuchung. Die Bedeutung des Stichprobenumfangs hängt dabei jedoch von den beiden anderen Faktoren ab. Bei explorativen Studien kann die Anzahl der UntersuchungsteilnehmerInnen sehr klein ausfallen, wenn aus den Ergebnissen nicht auf eine Grundgesamtheit geschlossen werden soll. Das kann z. B. dann der Fall sein, wenn die explorative Studie lediglich dem Ziel dient, Hypothesen zu generieren, die dann anschließend an einer größeren Stichprobe empirisch überprüft werden. Oder, um ein anderes Beispiel zu nennen, wenn bei einer Voruntersuchung vor der Durchführung des (Haupt-)Experimentes die unabhängigen Variablen (das Vorgehen bei der Herstellung der Wenn-Bedingungen) und die abhängigen Variablen (das Vorgehen bei der Messung der Dann-Folgen) auf ihre Zuverlässigkeit exemplarisch überprüft werden sollen. Auch in diesem Falle ist die Zuverlässigkeit dieser Instrumente in der späteren Hauptuntersuchung zu bestätigen.