Àngel Berna Prats - Introducció a l'enginyeria dels reactors químics

2. En la bibliografia sol trobar-se el valor de D 121, és a dir, a 121 ºC (el concepte de D s’ha exposat en el problema 1, que és el valor típic de la temperatura en el procés d’envasament. La variació de D amb la temperatura també sol expressar-se en funció d’una variable distinta a l’energia d’activació. Es tracta del paràmetre z , el significat del qual és l’augment de la temperatura que redueix el temps necessari per a aconseguir una determinada conversió a la desena part. Trobeu la relació entre z i E . La destrucció de microorganismes del tipus C. botulinum presenta una energia d’activació de prop de 265-340 kJ/mol i un valor de z de 8-12 ºC; comproveu l’equació anterior amb aquestes dades.

3. La dimerització 2 A (g) → A 2(g,l) es porta a terme en un RFP a 298 K i 2 atm (reactor isoterm). La concentració de A 2creix al llarg del reactor, i comença a condensar quan aconsegueix la saturació. Si s’alimenta A pur al reactor, per a quin valor de la conversió comença a condensar? Nota . Pot considerar-se que la pèrdua de pressió en el reactor és menyspreable. La pressió de vapor de A 2a 298 K és 0.5 atm.

4. Una mescla formada per SO 2(28 %) i aire (72 % en volum) s’introdueix contínuament en un reactor de flux (continu) en el qual es desenvolupa la reacció SO 2+ 1/2 O 2↔ SO 3. Construïu una taula estequiomètrica en la qual es pose de manifest la influència del grau de conversió sobre els cabals molars i les concentracions de cada espècie. Finalment, representeu gràficament la variació de les concentracions amb X en el cas que la pressió total siga de 1485 kPa i la temperatura de 227 ºC. Comenteu els resultats. Dades i notes . Pot suposar-se comportament isoterm. Així mateix, es pot menysprear la caiguda de pressió del fluid en recórrer el reactor.

5. Es disposa dels següents valors de la conversió en l’equilibri per a la reacció elemental en fase aquosa A ↔ B, amb c Ao= 1 mol/L i c Bo= 0 mol/L. Calculeu el valor de la constant d’equilibri per a cada una de les temperatures. A partir d’aquesta informació, determineu el valor de la calor de reacció, comprovant que pot prendre’s com a constant. Dibuixeu un esquema de les corbes de r constant en el diagrama X-T per a aquesta reacció. Com canviaria X eper a un valor distint de c Ao? Produiria algun canvi la utilització d’un valor distint de c Bo? I la presència d’un inert? Com canviaria l’esquema anterior com a conseqüència d’un canvi en c Ao?

6. Per a la mateixa reacció del problema 5 es coneix que la corba de r = 1 talla l’eix d’abscisses en T= 66.4 ºC i la de r = 3 en T= 90 ºC. Quant valen l’energia d’activació i el factor preexponencial per a la reacció directa? Quant val l’energia d’activació de la reacció inversa? Si, a més a més, es considera que el punt (X = 0.14, T = 70 ºC) pertany a la corba de r =1, quant val el factor preexponencial de la reacció inversa?

Nota . r ve donada en mol/L s.

7. La reacció irreversible en fase gas catalitzada per un sòlid A + B → C + D es porta a terme de manera isotèrmica en un reactor diferencial que conté el sòlid com a rebliment. S’han obtingut els resultats que es mostren en la taula P2.7.

TAULA P2.7

Informació cinètica de la reacció A + B → C + D

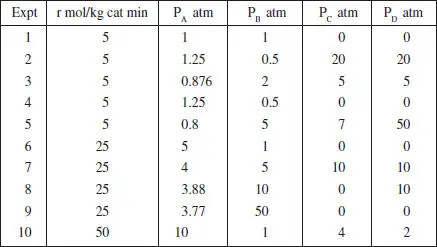
a) Quins experiments triaríeu per a determinar la influència de C i D sobre r ? Quina és aquesta influència?

b) Quins experiments triaríeu per a determinar la influència de A sobre r ? Quina és aquesta influència?

c) Coneguda la influència de A, C i D sobre r , què opineu sobre la influència de B? Creieu que és més complexa?

8. Considerem que la reacció irreversible en fase gas 2 A → B + C +3 D és de segon ordre en A. La mescla reaccionant inicial està formada per un 50 % de A i un 50 % d’inert. Si la reacció es desenvolupa mantenint constant la pressió i la temperatura, deduïu una expressió que mostre la variació del volum amb la conversió de A. Escriviu el model cinètic en funció també de la conversió.

9. Es disposa de la següent informació sobre la reacció en fase aquosa A 1↔ A 2. Coeficients cinètics: k = 3 10 7exp (-11600/RT) s -1, k’ = 1.6 10 18exp (-29600/RT) s -1. Calor de reacció = -18000 cal/mol.

a) Determineu la relació entre la constant d’equilibri K camb la temperatura.

b) Assenyaleu alguna raó per a suposar que el sistema es comportarà de forma ideal des del punt de vista termodinàmic.

c) Construïu el diagrama d’equilibri (taula i gràfica conversió temperatura), considerant que la composició de referència és: Concentració de A 1= 1 mol/L, i Concentració de A 2= 0.5 mol/L.

d) Calculeu i dibuixeu diverses línies de r constant en el diagrama anterior, mantenint les mateixes composicions de referència.

Lectures d’ampliació

AUCEJO A. i altres (1999): Introducció a l’Enginyeria Química , Barcelona, Enciclopèdia Catalana.

CHEN, N. H. i R. ARIS (1992): «Determination of Arrhenius constants by linear and nonlinear fitting», AIChE Journal , 38 (4), pp. 626-628.

CUSACK, R. W. (1999 a ): «A fresh look at reaction engineering», Chemical Engineering, 106 (11), pp. 134-146.

—(1999 b ): «Reaction engineering. Part 2. Choosing the right reactor», Chemical Engineering , 106 (13), pp. 80-85.

DREAM, R. F. (1999): «Heat transfer in jacketed vessels», Chemical Engineering 106 (1), pp. 90-96.

FONTIJN, A. i W. FEIDER (1977): «HTFFR kinetics studies of Al + CO 2→ AlO + CO from 300 to 1900 K, a non-Arrhenius reaction», Journal of Chemical Physics , 67 (4), pp. 1561-1569.

MODELL, M. i R. C. REID (1974): Thermodynamics and its applications , Englewood Cliffs, New Jersey, Prentice Hall.

SMITH, W. R. i R. W. MISSEN (1979): «What is chemical stoichiometry?», Chemical Engineering Education , 13 (1) pp. 26-32. Una versió més actualitzada es pot trobar en: Chemical reaction stoichiometry (CRS) tutorial, Java applet, and resources, http://chemengineer.about.com/science/chemengineer/gi/dynamic/offsite.htm?site=http%3A%2F%2F www.chemical-stoichiometry.net%2Ftutorial.htm.

STEVE, E. H. (1997 a ): «More reactor design considerations. Part 2», Chemical Engineering , 104 (12), pp. 100-102.

—(1997 b ): «Reactor design considerations. Part 1», Chemical Engineering , 104 (12), pp. 96-99.

—(1998 a ): «Aspect ratio and jacket zoning in reactor scale-up. Part 4», Chemical Engineering , 105 (1), pp. 96-98.

—(1998 b ): «Jacket zoning in reactor scale-up. Part 3», Chemical Engineering ,105 (1), pp. 92-95.

3. Reactors ideals. Comportament isoterm

3.1 Introducció

En el capítol anterior s’han estudiat els conceptes bàsics per a poder abordar l’anàlisi i el disseny d’un reactor ideal. Aquest model estarà format, principalment, pels balanços de matèria i energia, així com per les equacions de velocitat i les restriccions.

Les equacions dels balanços són equacions algebraiques o diferencials, en les quals participen (en ambdues) la composició ( X en el cas més simplificat) i la temperatura.