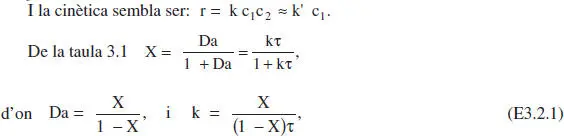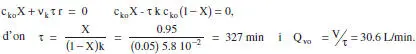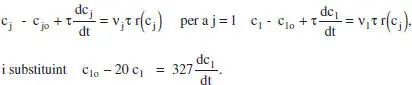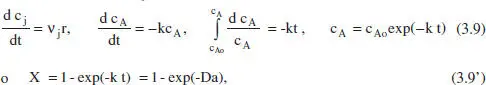Àngel Berna Prats - Introducció a l'enginyeria dels reactors químics

3.2.4 Producció

En aquest cas, la producció serà el cabal de producte (P) que s’obté del reactor, d’acord amb l’equació (2.39):

on es pot veure que per a una gran producció es necessita disposar d’un volum de reacció elevat i/o d’una elevada velocitat de reacció.

Exemple 3.2

La hidròlisi de solucions aquoses dilu'ides d’anhídrid acètic té Hoc d’acord amb l’esquema (CH 3CO) 2O(1) + H 2O(1) → 2 CH 3COOH (1). La reacció és irreversible i de segon ordre (de primer ordre parcial respecte de cada un dels reactius). Tanmateix, com que 1'aigua actua com a dissolvent també i està en gran excés, podem considerar-la únicament de primer ordre respecte de l’anhídrid. La cinètica de la reacció s’ha estudiat en un RCTA de 1.8 L de volum que funciona de forma isoterma. Els resultats d’una sèrie d’experiments es mostren a la primera part (primeres quatre columnes) de la taula E3.2. Comproveu que la reacció està ben representada per la cinètica proposada, calculeu la constant de velocitat de reacció a cada temperatura i l’energia d’activació d’aquesta.

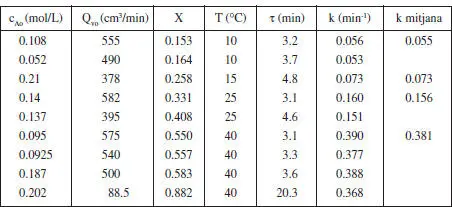
TAULA E3.2 Resultats d’una anàlisi cinètica de la hidròlisi de solucions aquoses diluïdes d’anhídrid acètic. Les quatre primeres columnes de la taula són els valors experimentals, les altres dues columnes són valors calculats a partir dels anteriors. L’última columna de la taula conté les mitjanes de k per a cada temperatura

Solució:

Com que de cada experiment tenim una velocitat de reacció, es tractarà d’avaluar el coeficient cinètic per a cadascun d’ells. Comprovarem que és de primer ordre observant que aquell coeficient pren pràcticament el mateix valor per a cada temperatura. Així mateix, si els valors de k varien amb la temperatura d’acord amb 1' equació d’Arrhenius, n’estarem més segurs.

La reacció és (CH 3CO) 2O(1) + H 2O(1) → 2CH 3COOH(1), és a dir, -A 1, - A 2, + 2 A 3= 0.

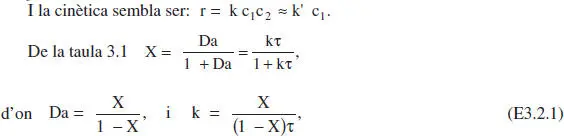
d’aquesta manera, per a cada valor de Q vo(o el que és el mateix, de τ) hem calculat el valor de k. Es pot veure que els valors de k són pràcticament coincidents per a cada temperatura, en la taula E3.2 es mostren els valors mitjans. Aquests valors segueixen el model d’Arrhenius, els paràmetres d’aquest model són: A = 4.68 10 7min" 1, i E = 11579 cal/mol.

Exemple 3.3

La descomposició irreversible de A 1s’efectua en presència d’una altra espècie qufmica A 2que actua com a catalitzador (romanent constant la seua concentració al llarg de la reacció). Experimentalment, s’ha trobat la segtient equació de velocitat per a la citada reacció: r = 1.30 c 1c 20 1/2, on r ve expressada en mol/L min, i c 1, i c 20en mol/L.

En un RCTA, de 10 m 3, es vol descompondre A 1en dissolució, en presència del catalitzador mencionat, que es trobarà present amb una concentració de 0.002 mol/L.

a) Si es vol que el corrent que s’extrau del reactor, quan funciona en règim estacionari, no continga més del 5 % de la quantitat del component A present en el corrent aliment, quin cabal volumètric s’ha d’introduir al reactor?

b) Si en la posada en marxa del reactor aquest s’ompli ràpidament fins al seu volum total amb la dissolució aliment, continuant introduint aquest amb el cabal calculat en l’apartat anterior, quant de temps haurà de transcórrer fins que la concentració de A en el corrent que s’extrau del reactor continga un percentatge de A, igual al 6% del que està present en 1'aliment?

Solució:

El model cinètic per aquesta reacció és r = 1.30 c1C2o 1/2= 5.810 -2c 1, (mol/L min) és doncs el d’una reacció de pseudoprimer ordre.

a ) El grau de conversió és del 95 %. El balanç de matèria queda

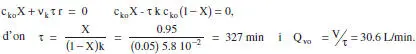
b ) Posar en marxa el reactor. Temps necessari per tal que X = 0.94. Cal analitzar el problema considerant règim no estacionari (si el sistema s’ha omplit i sobre'ix el mateix cabal que entra, és a dir, Q v= Q vo, V = constant):

De (2.54):

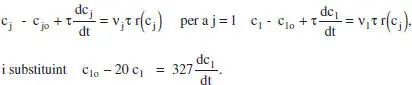
Amb les condicions inicials (en el reactor): a t = 0, c j= c’ jo. En aquest cas, c 1= c’ lo= c lo.

La solució de l’equació diferencial és c 1= c lo[0.05 + 0.95exp(-0.061 t)], d’on el temps necessari perquè c 1= 0.06 c lo, és 74.4 min. El temps per a assolir una conversió del 95 % seria infinit.

3.3 RDTA

3.3.1 Sistemes d’intercanvi de calor

L’aspecte d’aquest reactor és molt semblant al del RCTA, però es diferencia en 1’absèntia de corrents d’entrada i eixida, i en el fet que el seu comportament és sempre en estat no estacionari. Aquestes condicions canviants amb el temps faran que el flux de calor intercanviat per a mantenir constant la temperatura haurà d’evolucionar també amb el temps. Tot això fa que aquest comportament siga fàcil de calcular, però més difícil de portar a la pràctica. Aquesta dificultat rau en el fet d’haver de dosificar el flux de calor intercanviat al llarg del procés (q) . Aquesta dosificació s’aconseguirà modificant algunes de les variables que afecten q (el cabal i la temperatura del fluid bescanviador, Farea d’intercanvi, etc.).

Aquestes afirmacions poden xocar un poc amb la nostra experiència quotidiana al laboratori, en el qual s’utilitzen freqüentment aquests reactors de forma isoterma, la qual cosa s’obté introduint el reactor en un bany amb regulació de temperatura. Cal tenir en compte que en aquests aparells s’està malgastant un flux d’energia cap a l’ambient, que no seria permissible a una escala superior.

3.3.2 Relació X-t, per a distintes cinètiques

A tall d’exemple es mostrarà l’aplicació del model del balanc. de matèria a una cinètica de primer ordre. Suposem que es tracta d’un sistema de densitat constant.

Reacció: A → productes, r = k c A.

Aplicant el balanç de matèria, equació (2.42):

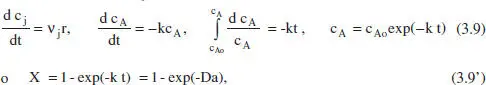
on és fàcil adonar-se que el grau de conversió, per a aquesta cinètica, és independent de la concentració inicial. La representació d’aquesta equació es pot veure en la figura 3.3. En la taula 3.1es poden veure algunes de les equacions resultants per a diferents cinètiques.

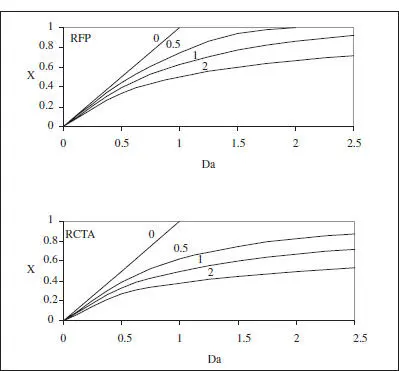
Figura 3.3. Variació de la conversió amb el temps espacial ( Da ) en un RFP (RDTA) i en un RCTA per a una reacció irreversible. El paràmetre indica l’ordre de la reacció.