Àngel Berna Prats - Introducció a l'enginyeria dels reactors químics

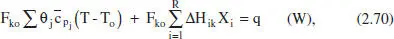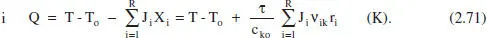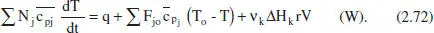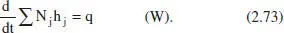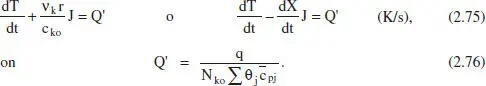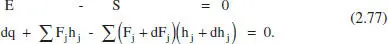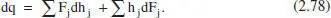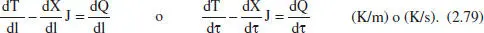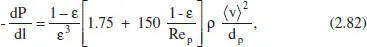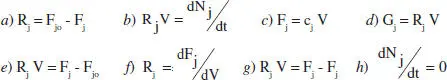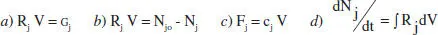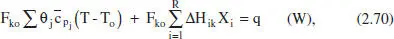
i

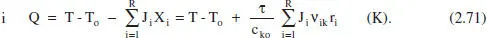
2.6.2.2 RCTA en estat no estacionari o RSCTA

L’equació (2.65) seria aplicable directament a un RCTA en estat no estacionari i a un RSCTA (reactor semicontinu de tanc agitat). Amb algunes transformations, es té:

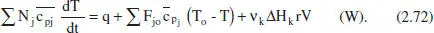
2.6.2.3 RDTA

De F I’equació (2.65), i considerant que no hi ha entrada ni eixida, es té:

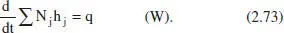
I desenvolupant aquesta equació com en el cas anterior:

on es posa de manifest que l’evolució de la temperatura en el reactor es deu a les contributions dels efectes tèrmics de la reacció i de l’intercanvi. Desenvolupant aquesta equació en funció del grau de conversió, i considerant menyspreable la variació de la calor de reacció amb el temps (amb el canvi de temperatura associat), s’arriba a:

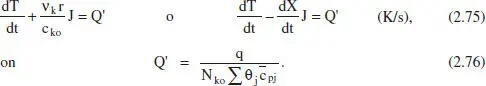
2.6.2.4 RFP o RCT

Si efectuem un balanc. d’energia en 1'element de volum dV (figura 2.15) en estat estacionari:

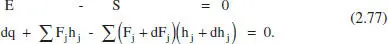
Desenvolupant el segon sumatori, simplificant i menyspreant els termes diferencials d’ordre superior, resulta:

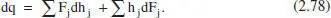
Reescrivint aquesta equació en funció del grau de conversió, per a sistemes en què només hi ha una sola reacció, i considerant menyspreable la variació de la calor de reacció amb la posició (amb el canvi de temperatura associat), s’arriba a:

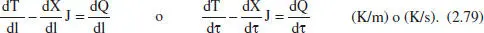
2.6.3 Balanç de quantitat de moviment

L’únic cas en què sol ser important aquest balang correspon al RFP (reactors tubulars), per ser utilitzat amb freqüencia per a reaccions en fase gas i estar constituït per conduccions de diàmetre xicotet. Atesa la influència de la pressió sobre la concentració, i d’aquesta sobre la velocitat de reacció, hauria d’incloure’s en el model.

Les equacions que permeten calcular la variació de la pressió al llarg del reactor són, entre altres:

– La de Haguen-Poiseuille, per a tubs buits i flux laminar (no és, per tant, un RFP):

on μ és la viscositat i < v > és la velocitat mitjana, ambdues del fluid. D és el diàmetre de la conducció (reactor).

– La de Fanning, per a tubs buits i flux turbulent:

on f és el factor de fricció i ρ la densitat del fluid.

– La d’Ergun, per a tubs amb farciment:

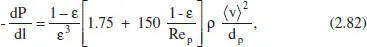
on ε és la porositat del llit i Re pés el mddul de Reynolds referit al diàmetre de la partícula (d p).

Qüestions, problemes i lectures d’ampliació

Qüestions

1. Quina de les següents expressions és 1'equació de disseny per a un RCTA? I quina ho és per a un RFP?

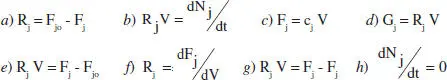
2. Una mescla de composició initial N joreacciona fins a un grau d’avanç ξ, i una altra de composició initial N’ joho fa fins a un grau d’avanç ξ, i llavors es mesclen. Demostreu que la composició que hi ha és la mateixa que si s’hagueren mesclat abans i reaccionaren fins a ξ £ ξ.

3. Seleccioneu la resposta més adequada per a les qüestions següents, raoneu moltbreument l’elecció.

α) Quina suposició s’ha fet per a modelitzar un RFP ideal?

a) Que el reactor ix bé en la foto.

b) Estat estacionari i cap variació radial.

c) Sistema gasós i estat estacionari.

d) Flux laminar i sistema gasós.

β) Quina de les següents afirmacions noés una de les característiques dels RCTA?

a) S’usen generalment per a mescles liquides.

b) Mescla intensa.

c) La concentració a l’eixida és igual a l’existent en el reactor.

d) Gradient de concentració axial.

4. Quina de les següents expressions és l’equació de disseny per a un RDTA?

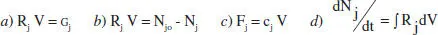
5. Estan tots els RTA perfectament mesclats?

a) Sí, els RTA són molt homogenis.

b) No, només els no ideals.

c) No, només els ideals.

d) No, només els que tracten sistemes líquids.

6. Assenyaleu de forma raonada entre les compositions següents les que no poden ser assolides. La reacció i la composició de partida es mostren en el problema 5. La temperatura d’operació és de 75 °C.

Problemes

1. La velocitat dels processos alimentaris no sol venir descrita en els termes convencionals de la cinètica química, probablement perquè el seu desenvolupament initial va correspondre a biòlegs o bioquímics i no a químics o enginyers químics. Així, una pràctica comuna en la indtistria alimentària consisteix a descriure la velocitat d’un procés en termes del paràmetre D , el temps de reducció decimal. Aquest concepte, per a una reacció del tipus Reactius → Productes, és el temps necessari perquè la concentració de reactius es reduïsca a la desena part del seu valor original. Trobeu la relació entre D i la constant cinètica k d’una reacció de primer ordre. La destrucció de microorganismes del tipus C. botulinum es pot representar d’aquesta forma, i per a aquesta reacció D val entre 0.1 i 0.3 min a la temperatura de referència (121 ºC), calcula els valors de k que li corresponen.