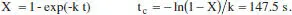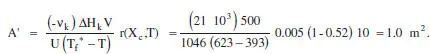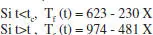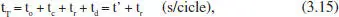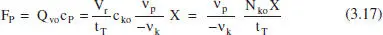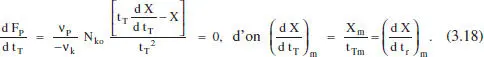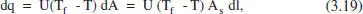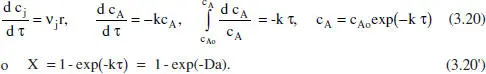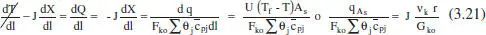Àngel Berna Prats - Introducció a l'enginyeria dels reactors químics

Cal veure si amb aquesta estratègia podem assolir la conversió desitjada (0.70). Per a aquest valor de X, T fresulta ser 462 K (< T f*). Per això, cal introduir alguna modificació per tal de poder operar el sistema. Aquesta modificació pot ser blocar una part de l’àrea d’intercanvi (pot tractar-se d’un sistema múltiple d’intercanvi, una de les parts del qual deixa de funcionar en qualsevol moment). Cal determinar, doncs, el moment en què s’ha de canviar de funcionament. Aquest moment serà quan s’assoleix la temperatura inferior per al fluid bescanviador.

Amb l’equació anterior, per a T f= 503 es té X = 0.52. Aquesta conversió s’assoleix en:

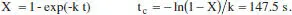
Si decidim que la temperatura en el moment del canvi assoleix de nou el seu valor màxim, la nova àrea serà:

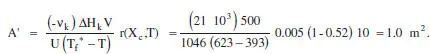
És a dir, cal blocar 1.2 m 2. Amb la qual cosa m’ = 9583 L s K/mol.

b ) Perfil Tf - X - t .

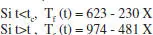
I, en tot cas, la variable temps vindrà donada per t = - ln(l - X)/k. Els resultats es poden veure en la figura 3.5.

3.3.4 Producció

Aquest sistema funciona per cicles. Cada cicle pot considerar-se format per les etapes següents: neteja i condicionament, ompliment, reacció i buidatge. Cada etapa consumeix una part del temps total del cicle. A més a més, només una d’aquestes etapes (la de reacció) pot considerar-se directament productiva, per això les altres es tracten com a temps mort (t’ ), encara que necessari:

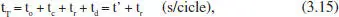
on t oés el temps de Fetapa de neteia i condicionament, t el de la de càrrega, etc. La relació existent entre el volum de reacció (un o diversos reactors funcionant de la mateixa manera) i el cabal de producció (m 3de la mescla reactiva/s) serà:

El flux molar de producte obtingut (suposant que a t = 0 no hi ha producte) serà

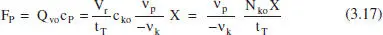
L’equació (3.17) facilita el càlcul del temps de reacció que correspon a la màxima producció, la qual cosa és una informació interessant. Per a valors xicotets d’aquesta variable ( t r) normalment es tenen valors grans de la velocitat de reacció, però encara s’aconsegueixen valors xicotets de X , de la concentració de producte i de la producció. Aquesta última per la importància de f ’ enfront de t r. Al contrari, per a valors grans de t res tenen valors xicotets de la velocitat de reacció, encara que X siga gran. El valor gran del temps farà que la producció siga reduïda. Pareix raonable que hi haja algun valor intermedi per al qual F psiga màxima:

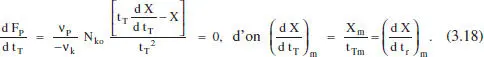
Això pot visualitzar-se gràficament tal com es mostra en la figura 3.6.

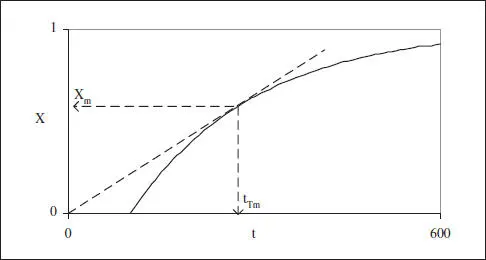
Figura 3.6. Condicions de producció màxima.

3.4 RFP

3.4.1 Sistemes d’intercanvi de calor

Ateses les característiques d’aquest reactor, els sistemes d’intercanvi seran externs, és a dir, Fintercanvi de calor tindrà Hoc a través de la paret. Els sistemes d’intercanvi seran: camises, resistències enrotllades, forns, etc.

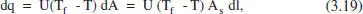
on T f= f(l), és a dir, la temperatura del fluid bescanviador ha de canviar d’una manera determinada al llarg del reactor per tal d’aconseguir el comportament isoterm. A sés l'area d’intercanvi per unitat de longitud de reactor (és a dir, el perfmetre).

3.4.2 Relació X-τ(Qvo, V), per a distintes cinètiques

Per a comprovar una vegada més l’equivalència entre aquest reactor i el RDTA, com correspon a la similitud dels models matemàtics, amb els canvis de les variables respectives τ per t r, es mostrarà l’aplicació del model del balanc. de matèria a una cinètica de primer ordre. Suposem que es tracta d’un sistema de densitat constant. Reacció: A → productes r = k c A.

Aplicant el balang de matèria, equació (2.58),

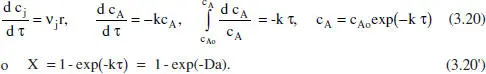
Equacions equivalents a les (3.9). En el capítol 3 de l’ Omnibook de Levenspiel (1993) es poden consultar les aplicacions d’aquests balangos a altres cinètiques. En lay taula 3.1es comparen algunes de les equacions obtingudes per a distintes cinètiques i els diferents reactors ideals.

3.4.3 Flux de calor intercanviat

Per a calcular el flux de calor [q = f(l) = f(V) = f(x)] necessari per a mantenir el comportament isoterm s’utilitzarà el balanc. d’energia combinat amb el de matèria. Així, de l’equació (2.79):

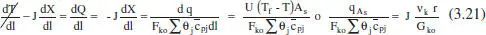
Com que r variarà amb la composició (excepte si la reacció és d’ordre zero), i aquesta ho fa amb la posició, q (és a dir, la parella U-Tf o bé qA) s’haurà d’adaptar a aquesta evolució. Per això, la solució del balang de matèria ens informarà de la variació de la composició (X) al llarg del reactor ( l o τ), i l’equació (3.21) ens permetrà calcular el valor de q que cal intercanviar en cada posició del reactor.

3.4.4 Producció

Ací es poden repetir, amb algunes diferències, els comentaris efectuats per al RCTA. Conegut X, es pot calcular F p, o deixar F pen funció del volum del reactor. Per a un sistema amb una sola reacció, volums grans de reactor i velocitats de reacció grans permetran obtenir una elevada producció.