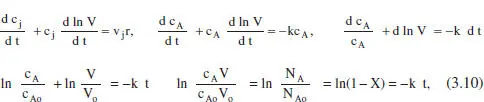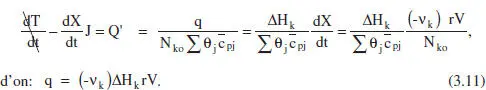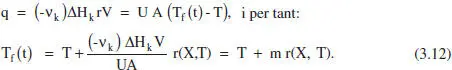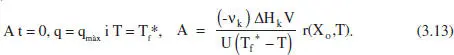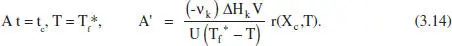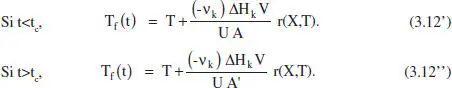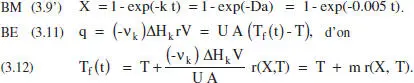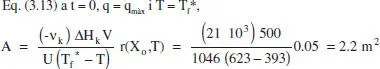Àngel Berna Prats - Introducció a l'enginyeria dels reactors químics

D’altra banda, si es tractara d’un sistema de densitat variable, prenent F equació (2.43) com a punt de partida:

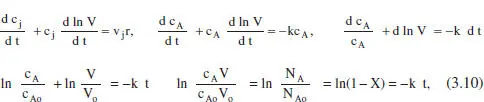
que donarà la relació cA-t. En aquest cas, la relació X-t , que es dedueix de F equació (3.10), és la mateixa que en el sistema de densitat constant. En el capítal 2 de F Omnibook de Levenspiel (1993) es poden consultar les aplicacions d’aquests balangos a altres cinètiques.

3.3.3 Flux de calor intercanviat

Per a calcular el flux de calor [q = f(t)] necessari per tal de mantenir el comportament isoterm s’utilitzarà el balang d’energia [equacions (2.75 i 2.76)] combinat amb el de matèria [equació (2.41)]:

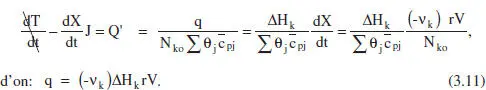
El flux de calor intercanviat és, doncs, proportional a la calor de reacció, al volum del sistema i a la velocitat de reacció. Com que la velocitat de reacció variant amb la composició (excepte si la reacció és d’ordre zero), i aquesta ho fa amb el temps, q s’haurà d’adaptar a aquesta evolució.

Si q és d’origen elèctric s’haurà de regular per a aquesta variació. Si s’utilitza un fluid bescanviador, q = U A (T f-T), l’evolució desitiada es pot obtenir, per exemple, modificant Tf(t) . Així, de l’equació (3.11):

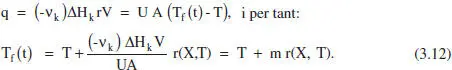
L’equació (3.12) mostra que Tf haurà de variar linealment amb la velocitat de reacció, r . Si la reacci6és endotèrmica (ΔH > 0), m > 0, Tf > T (es tractarà d’un fluid calefactor), en transcórrer la reacció (i el temps), X creix i r normalment disminuirà, amb la qual cosa Tf també ho farà. És a dir, les necessitats d’aportació calorífica van disminuint, i per això el fluid calefactor ho és cada vegada menys. Si la reacció és exotèrmica (ΔH < 0, Tf < T (es tractarà d’un fluid refrigerant), en transcórrer la reacció (i el temps), X creix i r normalment disminuirà, amb la qual cosa Tf augmentarà. És a dir, les necessitats d’eliminació de calor van disminuint, i el fluid refrigerant ho és cada vegada menys. Aquesta situació s’il·lustra en la figura 3.4, on es pot comprovar la disminució del valor absolut de la força impulsora (T f-T) durant l’operació d’un RDTA.

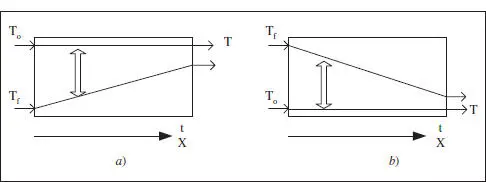
Figura 3.4. Evolució de T fdurant l’operació d’un RDTA. a ) Reacció exotèrmica, b ) Reacció endotèrmica.

En el cas d’una reacció endotèrmica, aquesta regulació es pot aconseguir actuant sobre la vàlvula que controla la pressió del vapor de calefacció; obrint progressivament aquesta vàlvula, disminuirà la pressió, i amb ella la temperatura de condensació.

Suposem, doncs, que es tracta d’una reacció endotèrmica i que es disposa de vapor de calefacció, la temperatura del qual es pot variar, tal com s’acaba d’exposar, entre T f*i T f *. Aquests límits vénen fixats per les limitacions de l’equipament de que es disposa. Com que al llarg del procés T f *ha de disminuir (figura 3.4 b ), pareix raonable començar en el valor màxim, T f *. Aquesta decisió permet determinar l’àrea d’intercanvi de calor necessària, aplicant l’equació (3.12) a Finstant inicial:

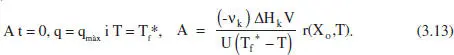
Amb aquest valor de A es pot determinar la variació de Tf durant la reacció. En el cas que Tf assolisca el valor mínim abans d’arribar a la conversió desitjada, es pot bloquejar una part del sistema d’intercanvi modificant simultàniament Tf. Els reactors grans poden tenir diferents zones d’intercanvi de calor per tal de poder adaptar-se a diferents situacions, per exemple diferents valors del flux de calor necessari o diferents volums de reacció. Si es decideix elevar de nou T fal seu valor màxim es tindrà

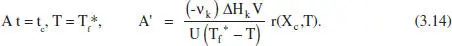
El temps en què té Hoc el bloqueig d’una part de l'area d’intercanvi és t c. L’àrea bloquejada serà ΔA = A - A’, i l’evolució de Tf vindrà donada per 1’equació (3.12) amb el valor adequat de l'area (figura 3.5). És a dir,

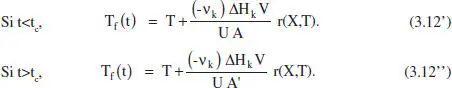
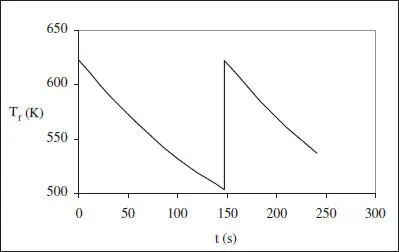
Figura 3.5. Evolució de T fdurant una reacció endotèrmica en un RDTA.

Exemple 3.4

Calculeu l’àrea o àrees de transmissió de calor necessària i les corbes temperature del fluid calefactor-grau de conversió-temps, en un RDTA en el qual es desenvolupa una reacció elemental irreversible, en fase líquida, de la forma: A 1→ A 2.

Dades i Notes . La reacció és endotèrmica, i la seua calor de reacció és a 393 K, de 21000 J/mol. La constant de velocitat val 0.005 s -1. El volum útil del reactor és de 0.5 m 3. La mescla que s’introdueix en el reactor conté 5 kmol de A . La temperatura de reacció serà 393 K, i es vol aconseguir un grau de conversió del 70 %. El coeficient global de transmissió de calor val U = 1046 W/m 2K. És acceptable la hipòtesi que es tracta d’un sistema de densitat constant. La calefacció s’efectuarà amb vapor de Dowtherm, la temperatura del qual pot oscil·lar entre 503 i 623 K.

Solució:

Dades: Esquema de reacció A 1→ A 2, reacció elemental, és a dir, de primer ordre. r = k c 1= 0.005 c lo(1 - X) (mol/s L). ΔH = 21000 J/mol (endotèrmica).

Reactor: RDTA isoterm a T = 393 K, V = 500 L, X = 0.70.

Aliment del reactor: N lo= 5 kmol, per tant c lo= N lo/V = 10 mol/L.

Sistema d’intercanvi de calor U = 1046 W/m 2K, i T fentre 503 i 623 K.

Model:

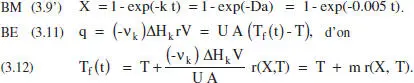
a ) Àrea o àrees de transmissió de calor.

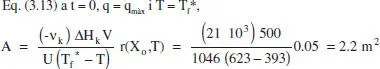
Amb la qual cosa m = 4600 L s K/mol.

Com es pot veure, s’ha fixat com a valor inicial de la temperatura del fluid bescanviador el valor més gran possible. Com que m >0 (reacció endotèrmica) aquesta temperatura anirà disminuint en avançar la reacció: