Bruno D´Amore - Los problemas de matemática en la práctica didáctica

1.3. Problem solving y problem posing

En este proceder a manera de espiral, encuentro la necesidad de contraponer dos problemáticas aparentemente opuestas, las del título de la sección.

Ya he hecho notar como uno de los impulsos para aprender es la motivación y la gratificación (placer ‘interno’, es decir satisfacción interna, o el reconocimiento social de ser considerado un buen solucionador de problemas). Por tanto, aparte de la motivación, la actividad de la resolución de problemas puede con razón ser considerada una extensión del aprendizaje de reglas o de maneras de comportarse o de obtención de ejemplos y estrategias, etc.

Tal proceso, difícil de definir, en su mayoría se desarrolla dentro del alumno que lo resuelve, aun cuando las sugerencias que llegan al sujeto que está resolviendo el problema sean notables (facilidades, sugerencias, etc.) bajo la forma de varios tipos de comunicación (verbal o no).

Por muy importante que sea la aplicación de reglas (normas, experiencias, […]) precedentes, vale la pena resaltar que el proceso resolutivo genera también y sobre todo un nuevo aprendizaje. Es cierto que, en primera instancia, aquel que resuelve intenta aplicar reglas (normas, experiencias, […]) precedentes (mejor aún si fueron exitosas); pero también es cierto que, si la situación problemática es oportuna, el sujeto podría no encontrar simplemente una solución análoga o idéntica a una precedente. En cambio, puede encontrar una combinación particular de reglas (normas, experiencias, […]) del todo nueva que enriquecerá el campo de la experiencia y a la cual se puede recurrir en el futuro. En fin, una frase en la que creo firmemente: resolviendo un problema, el sujeto aprende.

En este sentido, el modelo de referencia al que nos aferramos no tiene importancia, si es el de Dewey (1910) o en cambio el primero o el último de Gagné (1962, 1976); la cuestión es muy general y puede funcionar en todos los casos.

Por ahora, podemos llamar a esta serie de fragmentos “estrategias de resolución de problemas”:

• exploración de las reglas (normas, experiencias, [...]) ya conocidas y ya aplicadas;

• descarte de cada una;

• análisis de la situación desde varios puntos de vista;

• construcción de una regla completamente nueva, obtenida de la “dosificación” en manera oportuna de reglas (normas, experiencias, […]) usadas precedentemente;

• verificación de la capacidad de resolver el problema con la regla nueva.

Esta es la razón por la cual Gagné subraya la exigencia que «la expresión problem solving sea usada en general para referirse a problemas nuevos» (nosotros diremos: a verdaderos problemas y no a ejercicios). Él ejemplifica, entre estos, los siguientes: parquear el carro en un lugar permitido y cercano al lugar de trabajo; entender por qué suceden las fases lunares; describir un comportamiento indolente mediante las acciones de un personaje; (…) El hecho que la resolución induzca al pensamiento nos hace hablar de problem solving productivo (precisamente porque se produce un efecto).

Finalizados estos ejemplos, por así decirlo, de la vida real, Gagné (1976) pasa a problemas más cercanos a la praxis escolar, explicando bien la diferencia que hemos indicado mediante la dicotomía problema/ejercicio, pero lo ejemplifica también mediante juegos de cambios de lugar de fósforos, lo que ha sido analizado en modo particular desde un punto de vista psicológico por George Katona (1967). En este estudio, Katona sugiere una sucesión de métodos usados para hacer que los sujetos resuelvan problemas-juego con fósforos:

• hacer los movimientos precisos frente a los ojos del sujeto examinado, haciendo que este último recuerde los movimientos exactos;

• exponer verbalmente las propiedades “matemáticas” de los fósforos en cuestión, notando cómo los fósforos con “funciones” dobles deben ser movidos para tener una función “simple” o haciendo desaparecer por completo las figuras para hacer reconstruir la estructura deseada, con los vínculos deseados;

• proceder al descubrimiento guiado (ésta es la denominación usada): sin enunciar las reglas, proceder paso a paso, ilustrando los cambios producidos, dejando vacíos en la figura original.

Esta sucesión no es casual; según Katona el primer método lleva a un aumento banal de las capacidades; el segundo es mucho mejor; pero solo el tercero, en el cual el sujeto mismo descubre la regla, lleva a poseer satisfactoriamente la competencia. La enunciación verbal de la regla, que sin dudas produce efectos positivos, ayuda a muchos sujetos, pero no a otros. Haber descubierto por sí mismo la regla a aplicar, aún en contextos limitados, produce conocimientos y competencias en todos. Gagné (1973) ilustra otros ejemplos, además de aquel de Katona, entre los que se encuentra el experimento del péndulo de N. R. F. Maier, el cual describiré en breve.

Los resultados de tales experimentos se pueden condensar de la siguiente manera: se produce un efecto positivo en el sujeto que resuelve si se dice exactamente la naturaleza de la actuación (performance) que de él se espera; incluso si no se hace explícitamente, se puede dar una guía en cuanto a la elección de reglas (normas, experiencias, […]) que son útiles para escoger la estrategia, mediante la formulación del problema.

Toda la actividad y la atención del problem solving radican en la resolución.

De otra naturaleza, pero siempre dentro de la misma problemática, es la actividad del problem posing. Esta actividad involucra dos maneras diferentes, pero estrechamente interconectadas, de actuar:

• la creación de un problema basado en la reflexión relativa a un tema de examen;

• la propuesta de las preguntas que analizan situaciones “limítrofes” (externas pero cercanas) a un problema de examen.

Los autores del texto que volvió famoso el problem posing, S. I. Brown y M. I. Walter (1988), distinguen dos modos de actuar diferentes:

• hacer o hacerse preguntas

• preguntarse siempre «¿Y si (...) ?», o «¿Y si no (...) ?»

lo cual da muy buena cuenta de la cuestión.

Una reducción didáctica trivial del problem posing es la actividad consistente en hacer que los alumnos inventen los problemas: ésta ha sido ampliamente estudiada en la investigación en Didáctica de la Matemática y tendremos ocasión de entrar en detalles. Pero el problem posing, en su formulación más general y genuina, debe llevar a nuevos problemas, si bien generados a partir de aquellos presentes en situaciones anteriores. Este tipo de actividad lleva a generar un descubrimiento y en este sentido, a mi modo de ver, se asemeja mucho al que los estudiosos del problem solving han resaltado.

Dado que tendré que retomar este argumento en la siguiente sección, me limitaré a presentar este boceto a manera de resumen.

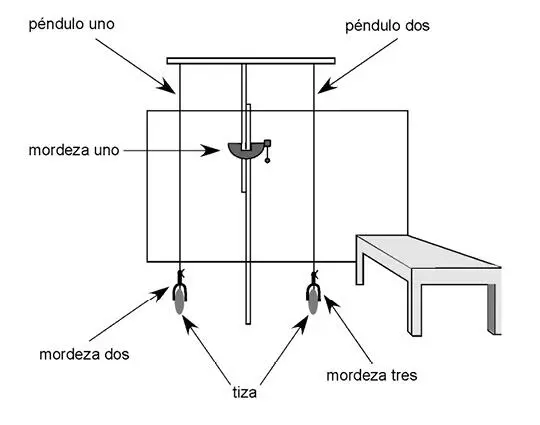
Experimento del péndulo de Maier del 1930, (Gagné, 1973).

El sujeto examinado es conducido a una habitación de 5 m por 6 m aproximadamente, en la que hay una mesa de trabajo. El sujeto tiene a su disposición tablillas, pedazos de hilo, tiza y abrazaderas. El problema es descrito en estos términos: construya dos péndulos, de manera que cada uno, oscilando y teniendo en cada extremidad una tiza, marque un punto establecido sobre el piso.

Para ilustrar mejor el problema, he aquí la representación de una buena solución proporcionada por sujetos sometidos a la prueba.

Con algunos sujetos, Maier usó la estrategia de recordar problemas precedentes que, en este caso, son, por decirlo así, sub problemas: