Bruno D´Amore - Los problemas de matemática en la práctica didáctica

• cómo se hace una plomada, teniendo a disposición hilo, abrazaderas y tiza;

• cómo hacer un poste largo, teniendo a disposición dos postes cortos y una abrazadera;

• cómo anclar al techo un objeto prensado entre dos postes.

Maier hizo sugerencias sobre la resolución presentando otro problema: el problema sería más simple si existiese una puntilla y se pudiera clavar un poste al techo. El experimento de Maier mostró cómo las instrucciones adicionales, que permiten recordar soluciones parciales precedentes, llevaron a los sujetos a la resolución del problema con mayor frecuencia, en comparación con aquellos que escuchaban solo el enunciado del problema sin ayudas adicionales. La sugerencia sobre la puntilla (que Maier llamó “dirección”), favorecía más la probabilidad de resolución.

Nota bibliográfica

Para la redacción de esta sección, utilicé (Dewey, 1910; Aebli, 1961; Katona, 1967; Gagné, 1973; Brown, Walter, 1988).

1.4. Problem solving, problem posing y descubrimiento

Empezamos con un ejemplo:

Dados dos triángulos equiláteros, encuentre un tercero, cuya área sea igual a la adición de las áreas de los otros dos. (Tomado de: Brown, Walter, 1988, p. 157).

Dentro del espíritu del problem posing, en cada intento por resolver el problema propuesto se cumple un análisis preliminar. Cada alumno tiene su propia reacción. Se puede notar que faltan datos y por lo tanto preguntar cuál es la naturaleza de la pregunta; ¿Cuál(es) de la(s) propiedad(es) de los triángulos entra(n) en juego?, ¿se espera una solución geométrica (un dibujo), o una numérica? Es claro que cada solucionador puede escoger la estrategia más adecuada de acuerdo con su propio “estilo”. Por ejemplo, un alumno puede decidir que va a estudiar un caso particular con los triángulos dados, uno de lado 3 y el otro de lado 7 y proceder de tal manera, haciendo un dibujo y recortando pedazos de cartulina (el cálculo sugerido por los autores no es, ciertamente, adecuado para niños de escuela primaria, pero quiero resaltar un espíritu independiente de estas contingencias) o usando un software geométrico a este propósito. Sin embargo, pero, aunque se haya encontrado una solución (aproximada), ¿qué sucede si se cambian los datos inventados, 3 y 7?

Lo que quiero subrayar aquí es que el problem posing es una forma de ubicarse dentro del problem solving y que, por ende, las dos problemáticas no son opuestas, sino bastante cercanas. “Plantear un problema” es solo una manera de comprenderlo mejor, de analizarlo mejor; hacerse preguntas que parecerían (…) rebotar la solicitud, puede significar entrar en mayor confianza con el problema.

Por tanto, si se llega a la resolución del problema, el problem posing tiene un efecto a posteriori, porque las preguntas sobre el problema y sobre la solución proporcionada no cesan: ¿se podría hacer de otra manera?, ¿se podría usar otro dato?, ¿hay una manera general de resolver esta cuestión?, ¿alguien ha inventado este método?, ¿cuándo y por qué se planteó este problema? (…) En una situación simétrica se plantea el efecto a priori que es sustancialmente el análisis de todos los detalles del problema antes de proceder con la solución.

En definitiva, el problem posing se ubica dentro de la amplia problemática del problem solving y no se limita a ser simplemente interpretado como un “hacer que los niños inventen problemas”, actividad que, entre otras cosas, es significativa si se conduce de manera motivada y prudente.

A mi modo de ver, dentro de los ejemplos dados por los Autores citados, es pertinente hablar del célebre caso del niño Gauss, muy famoso en las escuelas italianas:

Calcular la suma de los números naturales de 1 a 100.

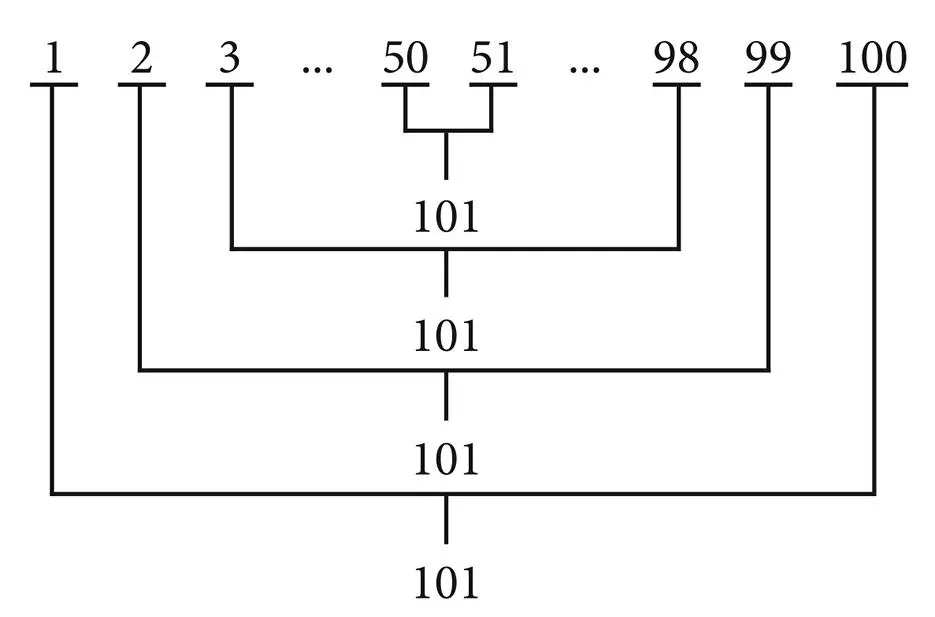
Es bien sabido que el procedimiento usado por Gauss es el siguiente: se observa que 1+100=101, 2+99=101, 3+98=101, y así hasta la última adición 50+51=101. Por lo tanto, la suma buscada se puede expresar como 50 veces 101. Éste es un buen ejemplo del problem solving que utiliza una manera de entender el problem posing, según lo que se ha dicho antes. En cambio de hacer lo que parece sugerir el texto del problema (es decir una secuencia absurda de cálculos 1+2=3, 3+3=4, 4+4=8, 8+5=13, haciendo 99 adiciones), analizamos el problema con “y si (...)”: «Y si en lugar de adicionar en orden, sumo el primero y el último, ¿qué encuentro?».

Entonces: se descubre una regularidad.

Se obtiene una regularidad adicionando en escala ascendente/descendente: hemos descubierto una regla («Una trampa» como dicen los niños). Pero para hablar de una regla, o de un descubrimiento, y proporcionarle dignidad en el mundo de la Matemática, es preciso que ésta sea general: ¿es siempre válida?, ¿si en lugar de 100 fuera 167?, ¿si en lugar de 1 partiéramos de 34?, ¿si en lugar de un número par tuviéramos un número impar? Y así sucesivamente.

Con base en las preguntas planteadas, hay una actitud analítica (llamémosla fantasía o curiosidad activas) que necesariamente hace que la resolución sea un descubrimiento.

El problem solving como método de aprendizaje exige que el sujeto descubra una regla de orden superior sin ayuda específica. Presumiblemente, el sujeto construye una nueva regla a su manera, aunque no esté en capacidad de comunicarla después de haberla descubierto. Ver específicamente Gagné (1973, p. 268). Este autor, haciendo referencia a los experimentos de Worthen, afirma que el método del descubrimiento (descrito anteriormente) lleva a un transfer amplio de las reglas adquiridas.

También en este caso, es importante señalar cómo la idea de la didáctica del descubrimiento se ha desacreditado en la práctica didáctica.

Las pruebas sobre el uso de los descubrimientos en el problem solving proporcionadas por los experimentos han ciertamente demostrado que las reglas de orden superior deben ser obtenidas mediante el descubrimiento. Muchas veces, por ejemplo, en el aprendizaje de los adultos, una guía llena de descripciones verbales puede ser tan completa que la regla a ser aprendida se enuncia verbalmente durante el proceso mismo de aprendizaje. La clave de la adquisición de una regla de orden superior no radica solamente en el método del descubrimiento. No obstante, la evidencia sugiere fuertemente que la adquisición de una regla de orden superior mediante el problem solving produce una capacidad muy eficiente, que permanece durante un período de tiempo importante. (Ver específicamente Gagné, 1973, p. 269; aquí Gagné cita estudios de Worthen, Shulman y Keislar, Ausubel, Gagné y Bessler, Guthrie, que no retomo en su totalidad).

Por lo tanto, se ve el problem posing como elemento determinante del proceso del problem solving y de preludio al descubrimiento.

Sin embargo, me parece honesto y necesario señalar que el problem solving no puede ser siempre exitoso. Por ejemplo, si las reglas a encontrar son de una complejidad superior a aquella a la cual puede llegar el sujeto, no se podrá tener más que una solución parcial (en casos particulares). Pero sobre este tema regresaré más delante.

Nota bibliográfica

Para la redacción de esta sección, hice uso de (Brown, Walter, 1988; Gagné, 1973).

Sobre el transfer, ver (Barth, 1990; Roveda, 1979).

1.5. Tipos de aprendizaje

Ya que resolver problemas es aprender, no resulta inútil, en este ámbito, analizar los diferentes tipos de aprendizaje; muchos estudiosos han buscado clasificaciones a propósito de este tema: entre las cuales se encuentra la afortunada descripción de Gagné (1973), expuesta brevemente en esta sección.