It remains to pick a suitable equilibrium state from the three we found in Sub section1.2.2. Of these, the most interesting is the one where the bead is not below or above point  . That is, consider the case where
. That is, consider the case where
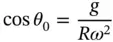
With a little effort and use of one trigonometric identity, you can show that the linear equation of motion about this state can be written as
(1.63) 
As you will see later, this is the standard form for an undamped vibrational equation of motion. If the bead is in equilibrium and is disturbed away from equilibrium by a small angle, it will begin to oscillate with a frequency that can be determined directly from Equation 1.63. 9
1.3.2 Nonlinear Structural Elements
Making linear approximations to trigonometric functions is not the only consideration we have in creating linear differential equations of motion. Many times the physical properties of structural elements in the system are nonlinear. A rubber suspension element is a good example. Depending on how it is designed, it can be made to get softer or harder as it deflects. Note that “softer” and “harder” are non‐technical words relating to the stiffness of the element. Figure 1.6shows the characteristics of a “hardening” spring where the element gets stiffer as it deflects. The stiffness is measured by the local tangent to the curve.
The equilibrium solution to the nonlinear equation of motion will place the system in equilibrium at 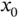 (the point labeled operating point on Figure 1.6). Once there, we consider motions
(the point labeled operating point on Figure 1.6). Once there, we consider motions 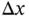 away from the operating point and use a Taylor's Series expansion for the nonlinear function
away from the operating point and use a Taylor's Series expansion for the nonlinear function 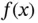
(1.64) 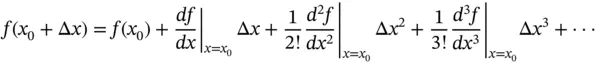
For small values of 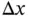 , we can neglect the higher order terms and write
, we can neglect the higher order terms and write
(1.65) 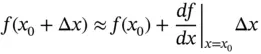
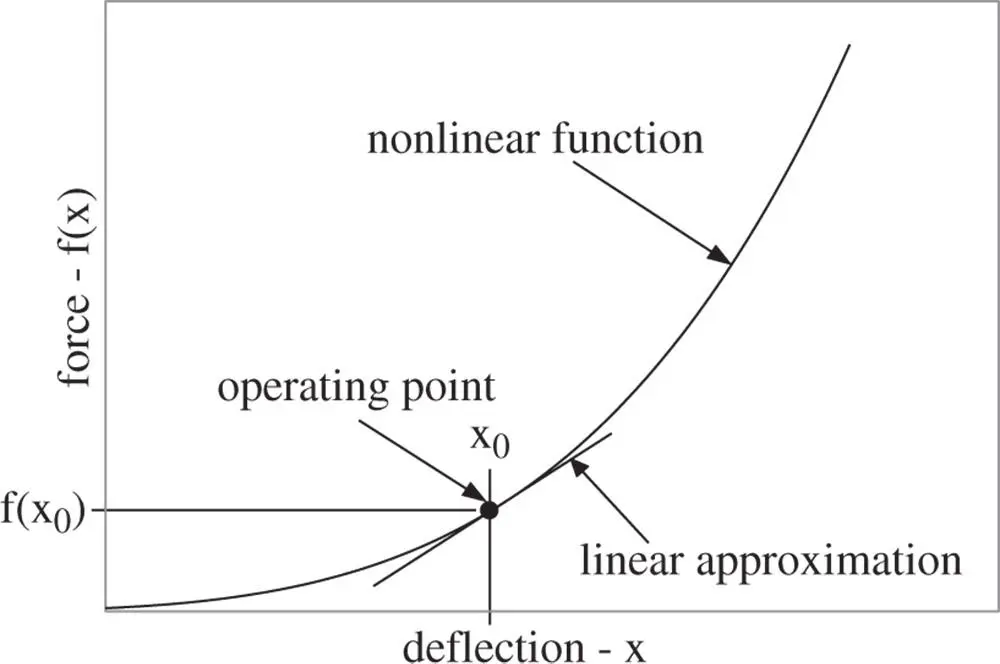
Figure 1.6 Nonlinear structural element – Linearization and effective stiffness.
where we can see that the linear term involves only the first derivative of the function. This derivative is the local tangent to the curve and is the effective stiffness of the element for this operating point. Linearization of functions about operating points is therefore an exercise in finding the local slope of the function and assuming that small deviations away from the operating point can be approximated by points lying on this straight line. The linear approximation is shown graphically in Figure 1.6.
The constant value of the force at the operating point 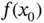 is the force acting at equilibrium and will enter the equation of motion in such a way that it and constant forces in other elements in the system will sum to zero. We consider these constant forces to be preloads on the elements and will quickly fall into the habit of leaving them out of the analysis because they always add up to zero.
is the force acting at equilibrium and will enter the equation of motion in such a way that it and constant forces in other elements in the system will sum to zero. We consider these constant forces to be preloads on the elements and will quickly fall into the habit of leaving them out of the analysis because they always add up to zero.
The study of Vibrations is the study of the behavior of dynamic systems as they experience small motions around stable equilibrium states. The steps in arriving at the governing equation 10of motion are
The nonlinear equations of motion for a system can be derived using either Newton's Laws or Lagrange's Equation.
The nonlinear equations of motion can be used to find equilibrium states for the system.
The degrees of freedom of the system can be replaced by their stable equilibrium values plus very small variables representing motions away from equilibrium.
The equations of motion can be linearized so that small motions about the stable equilibrium state are governed by linear, ordinary, differential equations.
1 1.1 The figure shows an undeflected, nonlinear spring on the left and the same spring, now deflected by the weight of the hanging mass, on the right. Taking the coordinate, , as the deflection of the spring from its free length, the force in the spring can be expressed aswhere is in Newtons and is in meters.Figure E1.1What will be the equilibrium value of for a mass of 1200 kg?What is the effective stiffness of the system for small motions around the equilibrium in part (a)?Plot the force versus deflection curve for the element. Show the operating point and the linear approximation to be used in the equation of motion.
2 1.2 The figure shows the force/deflection characteristic for hardening springs used to support a large machine in a factory. The force (F in Newtons) written as a function of deflection (x in mm) isFour mounts of this type are placed under the four corners of the machine and deflect 3 mm as they take up the weight.Figure E1.2What effective stiffness does the system have about equilibrium?What is the mass of the machine?
3 1.3 The effective stiffness of any object that deflects under the action of a force can be expressed as the ratio of that force divided by the resulting deflection. In some cases, there are good theoretical expressions that can be used to get the effective stiffness. A good example is the effective stiffness of a uniform beam. Suppose you have two identical lightweight, uniform beams of length and flexural rigidity . One of the beams is cantilevered and the other is simply supported. You have a choice of supporting a heavy piece of equipment at the end of the cantilevered beam or at the center of the simply supported beam. Which support has a greater effective stiffness? What is the ratio of the two effective stiffnesses?
4 1.4 An open cylindrical container with a weight at its bottom is placed in the ocean. The cylinder sinks until buoyancy forces equal the total weight and then floats upright in equilibrium.Draw a FBD of the cylinder just after it is placed in the water. Use a DOF, , to indicate the distance the bottom of the cylinder has traveled below the free surface of the water. There will be a buoyancy force acting upward on the cylinder. This force is due to the water pressure a distance under the surface. That pressure is equal to where is the density of water and is the acceleration due to gravity. Assume a cross‐sectional area of for the cylinder.Use Newton's Laws to write the equation of motion for the cylinder.Find the equilibrium condition for the cylinder and solve for , the equilibrium value of .
Читать дальше

 . That is, consider the case where
. That is, consider the case where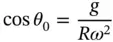

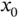 (the point labeled operating point on Figure 1.6). Once there, we consider motions
(the point labeled operating point on Figure 1.6). Once there, we consider motions 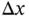 away from the operating point and use a Taylor's Series expansion for the nonlinear function
away from the operating point and use a Taylor's Series expansion for the nonlinear function 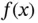
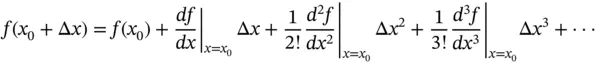
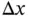 , we can neglect the higher order terms and write
, we can neglect the higher order terms and write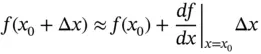

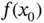 is the force acting at equilibrium and will enter the equation of motion in such a way that it and constant forces in other elements in the system will sum to zero. We consider these constant forces to be preloads on the elements and will quickly fall into the habit of leaving them out of the analysis because they always add up to zero.
is the force acting at equilibrium and will enter the equation of motion in such a way that it and constant forces in other elements in the system will sum to zero. We consider these constant forces to be preloads on the elements and will quickly fall into the habit of leaving them out of the analysis because they always add up to zero.










