Ronald J. Anderson - Introduction to Mechanical Vibrations

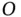The potential energy of the system is due to gravity only. If the datum for potential energy is taken to be at point , the potential energy, 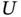, of the system is determined simply by the vertical distance from 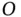to the bead. This distance is 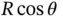and, as the mass is below the datum, the potential energy is negative, leading to

(1.21)

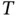Having expressions for and 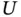and a single degree of freedom, 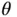, we can apply Lagrange's Equation ( Equation 1.16) and find

(1.22)

Substituting the expressions from Equation 1.22into Lagrange's Equation ( Equation 1.16) gives the desired equation of motion

(1.23)

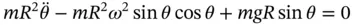
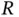where we note that this equation when divided throughout by yields the same result as Equations 1.11and 1.15, the equation of motion derived using Newton's Laws.

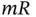Clearly, Equation 1.23could be further simplified by factoring out the group but this would take away the ability to look at the individual terms and give a physical explanation for them. Whenever an equation is derived, the first test for correctness is to see if all of the terms have the same dimensions. In this case, the first term has dimensions of 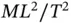where 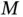is mass , 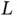is length , and 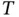is time . Note that angles such as 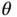are in radians, which are dimensionless since they are defined by an arc length divided by a radius. It follows that trigonometric functions such as 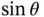and 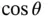are also dimensionless. Angular velocities therefore have dimensions derived from angles divided by time, 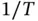, and angular accelerations are expressed as 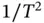. Using these conventions, it is easy to see that all three terms in Equation 1.23have the same dimensions 3 .

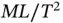The dimensions of force are or mass times acceleration. Taking this into account, we can see that the three terms in Equation 1.23all have dimensions of 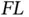or force times length. The terms are, in fact, all moments. The third term is the most obvious because it contains the gravity force 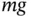multiplied by a moment arm of 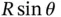. The moment arm is simply the horizontal distance between the mass and point 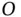. Lagrange's Equation has produced an equation of motion based on a dynamic moment balance about the stationary point 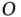and it did so without requiring the derivation of acceleration expressions, the drawing of free body diagrams, or the production of force and moment balance relationships. This is the power of using Lagrange's Equation for deriving equations of motion.

Following are explanations of terms that arise when using Lagrange's Equations.

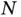The generalized coordinates are simply the degrees of freedom of the system with the condition that they be independently variable. That is, given a system with generalized coordinates ( 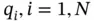), any generalized coordinate, 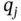, must be able to undergo an arbitrary small variation, 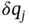, with all of the other generalized coordinates being held constant.

In the example just considered, we might try to specify the position of the bead on the wire by using two coordinates – the vertical distance from and the horizontal distance from . We would soon find that these coordinates are not independent because the bead is constrained to stay on the circular wire so changing the horizontal position requires a change in the vertical position. These two coordinates are therefore not generalized coordinates.