Ronald J. Anderson - Introduction to Mechanical Vibrations

Figure 1.3 A 2D representation of the bead on a wire.

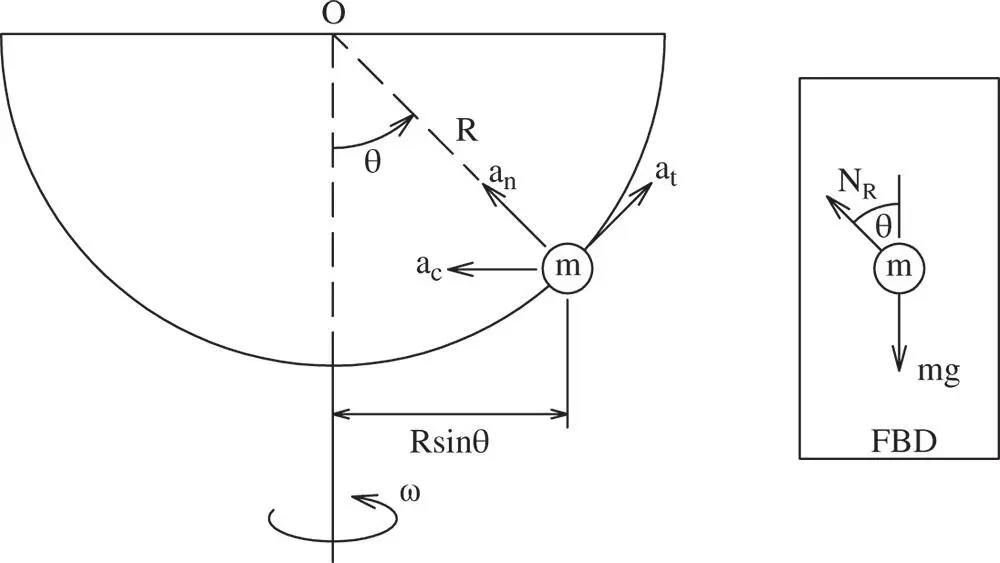
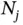The inset in Figure 1.3shows a FBD of the bead with the gravitational force and radial normal force being visible in this plane. There is another normal force perpendicular to the plane that can't be seen in this view. It is in Figure 1.2and was shown to be equal to 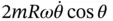in Equation 1.9. The acceleration in this expression is a Coriolis acceleration. One needs quite a lot of experience with kinematic analysis to get the correct form of this term using an informal approach. Thankfully, it is perpendicular to the plane in which the bead moves relative to the wire, so it never appears in the equation of motion 1 .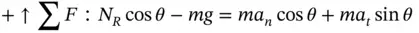

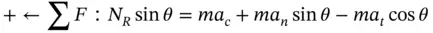
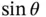Summing forces in the vertical and horizontal directions gives

(1.12)

(1.13)

To eliminate the constraining normal force from these two equations, we multiply Equation 1.12by and Equation 1.13by 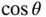and subtract the resulting expressions. The result is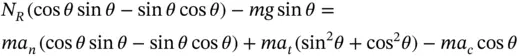

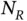(1.14)

where it is clear that both and 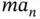are multiplied by zero and disappear from further consideration whereas 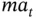is multiplied by a trigonometric identity equal to 1. Simplifying and substituting the derived kinematic expressions for 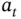and 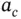gives

(1.15)

which is the same nonlinear equation of motion ( Equation 1.11) found in Subsection 1.1.1.

In this section, we consider the use of Lagrange's 2 Equations of Motion.

Lagrange's Equations, since they are based on work/energy principles, give the analyst two distinct advantages when deriving the equations of motion. First, the vector kinematic analysis is shorter than it is with a direct application of Newton's Laws since acceleration vectors need not be found. This is because the kinetic and potential energy expressions can be derived from velocity vectors and position vectors respectively. Secondly, there is no need to draw free body diagrams for each of the rigid bodies in the system because the forces of constraint between the bodies do no work and are therefore not required for the analysis.

Of course, there are also disadvantages. The method requires a great deal of differentiation, sometimes of relatively complicated functions. Some analysts prefer the kinematics of Newton's method over the differentiation required when using Lagrange's Equations. Some point to a lack of physical feeling for problems without free body diagrams as being a disadvantage of the method. Finally, if the intent of analyzing the dynamics of a system is to predict loads, which could be carried forward into a structural analysis for instance, the forces of interaction between bodies are not available from a straightforward application of Lagrange's Equations.

We consider again the bead on the semicircular wire ( Figure 1.1) and derive the equation of motion using Lagrange's Equations.

Lagrange's Equation is:

(1.16)

where:

= the total kinetic energy of the system

= the total potential energy of the system

= a generalized coordinate

= the time derivative of

= the generalized force corresponding to a variation of

We first determine the kinetic energy of the system. This requires that we have an expression for the absolute velocity of the mass. This was done previously and the result, from Equation 1.5, is

(1.17)

The kinetic energy of the system is then

(1.18)

which becomes, after substitution of Equation 1.17and some simplification,

(1.19)

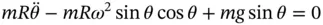
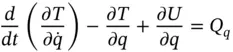
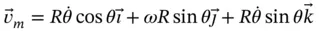
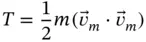
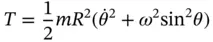
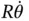Alternatively, using the informal approach and referring to Figure 1.3, we can see that there will be a component of velocity equal to tangent to the wire and another component equal to 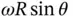perpendicular to the wire and into the page. These two components are mutually perpendicular so we can write, by applying Pythagoras' theorem,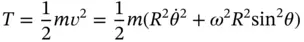

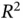(1.20)

After factoring out of the brackets, this becomes exactly the same expression we had in Equation 1.19.