1 Cover
2 Preface
3 About the Companion Website
4 1 The Transition from Dynamics to Vibrations 1.1 Bead on a Wire: The Nonlinear Equations of Motion 1.2 Equilibrium Solutions 1.3 Linearization 1.4 Summary Exercises Notes
5 2 Single Degree of Freedom Systems – Modeling 2.1 Modeling Single Degree of Freedom Systems Exercises Notes
6 3 Single Degree of Freedom Systems – Free Vibrations 3.1 Undamped Free Vibrations 3.2 Response to Initial Conditions 3.3 Damped Free Vibrations 3.4 Root Locus Exercises Notes
7 4 SDOF Systems – Forced Vibrations – Response to Initial Conditions 4.1 Time Response to a Harmonically Applied Force in Undamped Systems Exercises
8 5 SDOF Systems – Steady State Forced Vibrations 5.1 Undamped Steady State Response to a Harmonically Applied Force 5.2 Damped Steady State Response to a Harmonically Applied Force 5.3 Response to Harmonic Base Motion 5.4 Response to a Rotating Unbalance 5.5 Accelerometers Exercises Notes
9 6 Damping 6.1 Linear Viscous Damping 6.2 Coulomb or Dry Friction Damping 6.3 Logarithmic Decrement Exercises Notes
10 7 Systems with More than One Degree of Freedom 7.1 2DOF Undamped Free Vibrations – Modeling 7.2 2DOF Undamped Free Vibrations – Natural Frequencies 7.3 2DOF Undamped Free Vibrations – Mode Shapes 7.4 Mode Shape Descriptions 7.5 Response to Initial Conditions 7.6 2DOF Undamped Forced Vibrations 7.7 Vibration Absorbers 7.8 The Method of Normal Modes 7.9 The Cart and Pendulum Example 7.10 Normal Modes Example Exercises Notes
11 8 Continuous Systems 8.1 The Equations of Motion for a Taut String 8.2 Natural Frequencies and Mode Shapes for a Taut String 8.3 Vibrations of Uniform Beams Exercises Notes
12 9 Finite Elements 9.1 Shape Functions 9.2 The Stiffness Matrix for an Elastic Rod 9.3 The Mass Matrix for an Elastic Rod 9.4 Using Multiple Elements 9.5 The Two‐noded Beam Element 9.6 Two‐noded Beam Element Vibrations Example Exercises Notes
13 10 The Inerter 10.1 Modeling the Inerter 10.2 The Inerter in the Equations of Motion 10.3 An Examination of the Effect of an Inerter on System Response 10.4 The Inerter as a Vibration Absorber Exercises Notes
14 11 Analysis of Experimental Data 11.1 Typical Test Data 11.2 Transforming to the Frequency Domain – The CFT 11.3 Transforming to the Frequency Domain – The DFT 11.4 Transforming to the Frequency Domain – A Faster DFT 11.5 Transforming to the Frequency Domain – The FFT 11.6 Transforming to the Frequency Domain – An Example 11.7 Sampling and Aliasing 11.8 Leakage and Windowing 11.9 Decimating Data 11.10 Averaging FFTs Exercises Notes
15 12 Topics in Vibrations 12.1 What About the Mass of the Spring? 12.2 Flow‐induced Vibrations 12.3 Self‐Excited Oscillations of Railway Wheelsets 12.4 What is a Rigid Body Mode? 12.5 Why Static Deflection is Very Useful Exercises Notes
16 Appendix A: Least Squares Curve Fitting
17 Appendix B: Moments of Inertia B.1 Parallel Axis Theorem for Moments of Inertia B.2 Moments of Inertia for Commonly Encountered Bodies Notes
18 Index
19 End User License Agreement
1 Chapter 6Table 6.1 Effective viscous damping coefficients.
2 Chapter 10Table 10.1 Inertia coefficients.
3 Chapter 11Table 11.1 Fourier Transforms Computational Effort.Table 11.2 Sampled Data.Table 11.3 DFT Coefficients.Table 11.4 DFT Coefficients.
4 Chapter 12Table 12.1 The Routh Table.Table 12.2 The Routh Table for the wheelset.
5 Appendix ATable A.1 Sample data points.
1 Chapter 1 Figure 1.1 A bead on a wire. Figure 1.2 Free Body Diagram of a bead on a wire. Figure 1.3 A 2D representation of the bead on a wire. Figure 1.4 A linear viscous damper. Figure 1.5 A simple pendulum. Figure 1.6 Nonlinear structural element – Linearization and effective stiffn... Figure E1.1 Figure E1.2 Figure E1.5 Figure E1.6
2 Chapter 2 Figure 2.1 A mass on a spring. Figure 2.2 Independent front suspension. Figure 2.3 Assembly of the mass/spring system. Figure 2.4 FBD of the mass/spring system. Figure 2.5 A spring element. Figure 2.6 The linear spring constitutive relationship. Figure 2.7 A mass on a spring. Figure 2.8 A mass on a spring – FBD. Figure 2.9 A simple pendulum.Figure 2.10 Spring deflection due to a large angle of rotation.Figure 2.11 A body with a rotational DOF: How to deal with a spring, a dampe...Figure 2.12 Gravitational effects.Figure E2.2 Figure E2.3 Figure E2.4 Figure E2.5 Figure E2.6
3 Chapter 3Figure 3.1 Simple harmonic motion.Figure 3.2 Simple harmonic motion with a phase shift.Figure 3.3 Mass/spring/damper system.Figure 3.4 Mass/spring/damper FBD.Figure 3.5 The underdamped response.Figure 3.6 The critically damped response.Figure 3.7 The overdamped response.Figure 3.8 The root locus.Figure E3.1 Figure E3.2 Figure E3.3 Figure E3.4 Figure E3.5 Figure E3.6 Figure E3.7
4 Chapter 4Figure 4.1 SDOF system with a harmonically applied force.Figure 4.2 SDOF system with a harmonically applied force – FBD.Figure 4.3 Widely separated frequencies.Figure 4.4 The Beating phenomenon.Figure 4.5 Resonance.Figure E4.2
5 Chapter 5Figure 5.1 SDOF system with a harmonically applied force.Figure 5.2 Frequency response – SDOF undamped system.Figure 5.3 Magnification Factor ‐ SDOF undamped system.Figure 5.4 Damped SDOF system with a harmonically applied force.Figure 5.5 Magnification Factor – SDOF damped system.Figure 5.6 Damped SDOF system with harmonic base motion.Figure 5.7 Free body diagram – damped SDOF system with harmonic base motion.Figure 5.8 Magnification Factor – Harmonic base motion.Figure 5.9 Force transmissibility – Harmonic base motion.Figure 5.10 Damped SDOF system with a rotating unbalance.Figure 5.11 Free body diagram – Damped SDOF system with a rotating unbalance...Figure 5.12 Amplitude Ratio – SDOF rotating unbalance.Figure 5.13 Schematic layout of a typical piezoelectric accelerometer.Figure 5.14 Model of a typical piezoelectric accelerometer.Figure 5.15 Free body diagram of the accelerometer model.Figure 5.16 Piezoelectric accelerometer – % error.Figure E5.1 Figure E5.3 Figure E5.8 Figure E5.9
6 Chapter 6Figure 6.1 A linear viscous damper.Figure 6.2 Test setup for energy removed by a linear viscous damper.Figure 6.3 Hysteresis loop for a linear viscous damper.Figure 6.4 Experimental hysteresis loops for two shock absorbers.Figure 6.5 Friction force magnitude and direction.Figure 6.6 A system with Coulomb friction.Figure 6.7 Response with Coulomb friction.Figure 6.8 The underdamped response.Figure E6.1 Figure E6.3
7 Chapter 7Figure 7.1 A 2DOF undamped system.Figure 7.2 Free body diagram for the 2DOF undamped system.Figure 7.3 First mode shape for the 2DOF undamped system.Figure 7.4 Second mode shape for the 2DOF undamped system.Figure 7.5 Another sample system.Figure 7.6 A 2DOF undamped, forced, system.Figure 7.7 A model of a machine experiencing large amplitudes.Figure 7.8 The machine with the vibration absorber mounted.Figure 7.9 The cart and pendulum system.Figure 7.10 The cart and pendulum system – FBD.Figure E7.1Figure E7.2Figure E7.3Figure E7.5Figure E7.6Figure E7.7
8 Chapter 8Figure 8.1 A taut string.Figure 8.2 The first five string modes.Figure 8.3 Deflections of a uniform beam.Figure 8.4 A beam element.Figure 8.5 A cantilever beam.Figure 8.6 The first three cantilever beam modes.
9 Chapter 9Figure 9.1 A beam element.Figure 9.2 A non‐uniform beam.Figure 9.3 An elastic rod.Figure 9.4 An elastic rod element.Figure 9.5 An element of the element.Figure 9.6 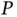 versus
versus 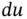 for the element.Figure 9.7 The rod element with nodal forces applied.Figure 9.8 A statically loaded rod modeled with one element.Figure 9.9 The velocity of the element of the element.Figure 9.10 Two rod elements in an assembly.Figure 9.11 Free body diagrams of the two rod elements.Figure 9.12 The global mass matrix.Figure 9.13 The global stiffness matrix.Figure 9.14 The two‐noded beam element.Figure 9.15
for the element.Figure 9.7 The rod element with nodal forces applied.Figure 9.8 A statically loaded rod modeled with one element.Figure 9.9 The velocity of the element of the element.Figure 9.10 Two rod elements in an assembly.Figure 9.11 Free body diagrams of the two rod elements.Figure 9.12 The global mass matrix.Figure 9.13 The global stiffness matrix.Figure 9.14 The two‐noded beam element.Figure 9.15 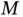 versus
versus 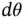 for the element.Figure 9.16 Node and element numbering.Figure 9.17 Node and element numbering.Figure 9.18 Externally applied forces and moments.Figure 9.19 The harmonically varying applied load.Figure E9.3 Figure E9.4
for the element.Figure 9.16 Node and element numbering.Figure 9.17 Node and element numbering.Figure 9.18 Externally applied forces and moments.Figure 9.19 The harmonically varying applied load.Figure E9.3 Figure E9.4
Читать дальше

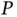 versus
versus 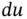 for the element.Figure 9.7 The rod element with nodal forces applied.Figure 9.8 A statically loaded rod modeled with one element.Figure 9.9 The velocity of the element of the element.Figure 9.10 Two rod elements in an assembly.Figure 9.11 Free body diagrams of the two rod elements.Figure 9.12 The global mass matrix.Figure 9.13 The global stiffness matrix.Figure 9.14 The two‐noded beam element.Figure 9.15
for the element.Figure 9.7 The rod element with nodal forces applied.Figure 9.8 A statically loaded rod modeled with one element.Figure 9.9 The velocity of the element of the element.Figure 9.10 Two rod elements in an assembly.Figure 9.11 Free body diagrams of the two rod elements.Figure 9.12 The global mass matrix.Figure 9.13 The global stiffness matrix.Figure 9.14 The two‐noded beam element.Figure 9.15 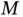 versus
versus 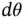 for the element.Figure 9.16 Node and element numbering.Figure 9.17 Node and element numbering.Figure 9.18 Externally applied forces and moments.Figure 9.19 The harmonically varying applied load.Figure E9.3 Figure E9.4
for the element.Figure 9.16 Node and element numbering.Figure 9.17 Node and element numbering.Figure 9.18 Externally applied forces and moments.Figure 9.19 The harmonically varying applied load.Figure E9.3 Figure E9.4










