Ronald J. Anderson - Introduction to Mechanical Vibrations

(1.53)

and the equation of motion ( Equation 1.51) becomes

(1.54)

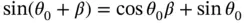
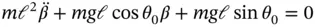
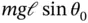Note the constant term that appears in Equation 1.54. This is the term that was set to zero to determine the equilibrium state (see Equation 1.45) and it is still equal to zero so it can be removed. The equilibrium condition is always a set of constant terms that must be zero for the system not to move and that set of constant terms always reappears in the linearized equation of motion. After removing the equilibrium condition, the linearized equation of motion for the pendulum becomes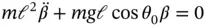

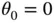(1.55)

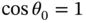This equation is valid for motion about either of the two equilibrium states we found (i.e. with and 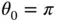with 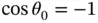). We write

(1.56)

and

(1.57)

Equation 1.56will yield oscillating solutions (i.e. vibrations – more to come later) and Equation 1.57will yield growing exponential solutions, showing that the system really doesn't want to stay in the unstable upright position.

The EOM for the bead on the rotating wire is

(1.58)

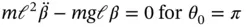
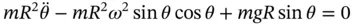
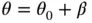As we did for the simple pendulum, we let where 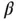is a small angle. Since 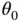is a constant, we differentiate to find that 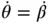and 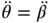. Substituting into Equation 1.58gives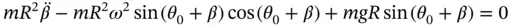

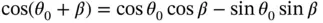
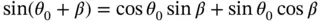
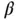
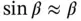
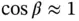
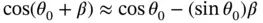
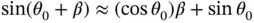
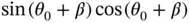(1.59)

We use the trigonometric identities

along with the linearizing approximations for the small angle

to get the linearized forms

Then, the term which appears in Equation 1.59can be approximated by the product of these two expressions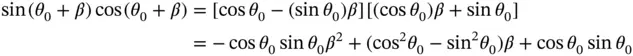

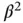(1.60)

We then say that the nonlinear term can be neglected as being negligibly small compared to the linear term 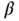since 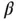is a small angle. This is at the heart of the linearization process. The linearized EOM becomes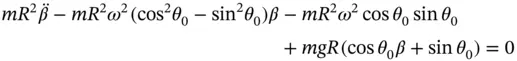

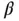(1.61)

Now we rearrange this to separate the constant terms from the terms with and its derivatives. The result is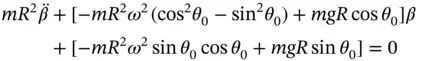

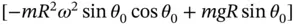(1.62)

where the constant term is exactly the same as the equilibrium condition stated in Equation 1.47and it is identically equal to zero by definition so it can be removed from the equation of motion. This will always be the case for vibrational systems. As we progress through the following chapters, we will often say something to the effect of “the gravitational forces are canceled out by preloads in the springs so they can be ignored” where we actually mean that our equations of motion are written for small motions away from an equilibrium state and that we need only be concerned with how the forces in elements change as the system moves slightly away from equilibrium. There will be forces holding the system in equilibrium and they may be large but they always add up to zero. The equilibrium condition for the bead is actually a statement that the moment that the gravitational force exerts about point 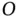is exactly equal and opposite to the moment about 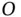due to the centripetal acceleration.